Линейные уравнения первого порядка ~ Общее решение однородного уравнения ~ Решение задачи Коши для однородного  уравнения ~ Общее решение  неоднородного  уравнения ~ Решение задачи Коши для неоднородного  уравнения

Уравнение вида

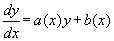
называется линейным неоднородным уравнением.
Уравнение вида

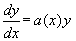
называется линейным однородным уравнением.

Очевидно, что однородное линейное уравнение является уравнением с разделяющимися переменными и его общее решение вычисляется по формуле

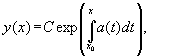
где C— произвольная постоянная,

ПРИМЕР 1. Общее решение линейного однородного уравнения первого порядка.

Решение задачи Коши  y(x₀) = y₀ определяется выражением

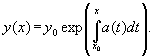
ПРИМЕР 2. Решение задачи Коши для линейного однородного уравнения первого порядка.

Метод вариации произвольных постоянных для линейного неоднородного уравненя состоит в том, что решение неоднородного уравнения записывается в виде

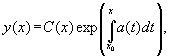
где C(x) неизвестная функция. Подставляя в уравнение имеем для C(x)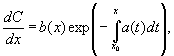
откуда

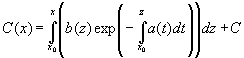
и тогда для общего решения неоднородного уравнения справедливо

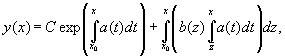
где C — произвольная постоянная.

ПРИМЕР 3. Общее решение линейного неоднородного уравнения первого порядка.

Для решения задачи Коши y(x₀) = y₀ для линейного неоднородного уравнения справедлива формула

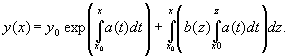
ПРИМЕР 4. Решение задачи Коши для линейного неоднородного уравнения первого порядка.