Уравнение в полных дифференциалах ~ Общий интеграл ~  Решение задачи Коши

Обыкновенное дифференциальное уравнение первого порядка вида
P(x, y) dx + Q(x, y) dy = 0
называется уравнением в полных дифференциалах, если P(x, y) и Q(x, y) непрерывны в некоторой односвязной области D и в этой области выполнено условие

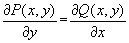
Тогда общий интеграл уравнения задается  выражением
.

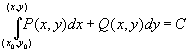Обозначим

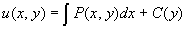
тогда

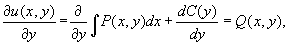
откуда

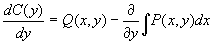
и формула для вычисления u(x, y) имеет вид:

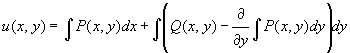
ПРИМЕР 1. Общий интеграл уравнения в полных дифференциалах.

Выражение u(x, y)=0, где

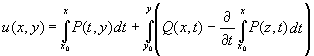
задает решение задачи Коши y(x₀) = y_0.

ПРИМЕР 2. Решение задачи Коши для уравнения в полных дифференциалах.