Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример 4

Пример 1. Виды фазовых кривых

Среди фазовых кривых автономной системы

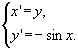
можно видеть фазовые кривые всех трех типов: точки, замкнутые гладкие кривые и гладкие кривые без самопересечений.
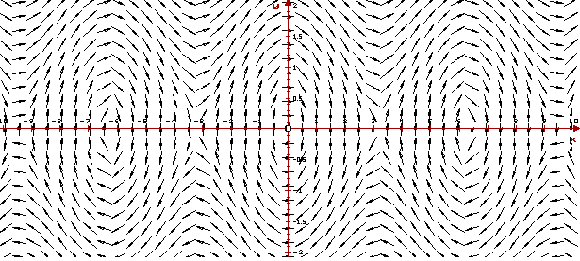
Ниже приведены, построенные программой ОДУ, векторное поле и фазовый портрет системы, на котором изображены фазовые кривые всех трех типов. Векторное поле показывает направление движения вдоль фазовых кривых с ростом t.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 2. Устойчивый предельный цикл

Автономная система

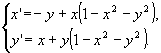
имеет устойчивый предельный цикл.
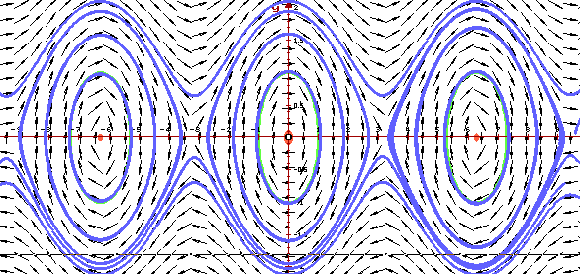
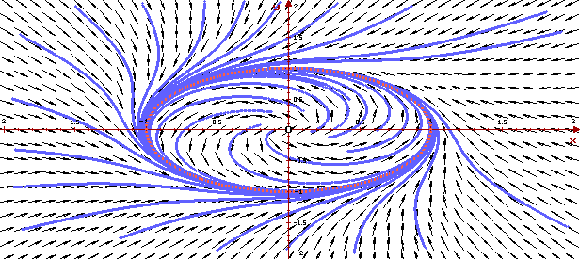
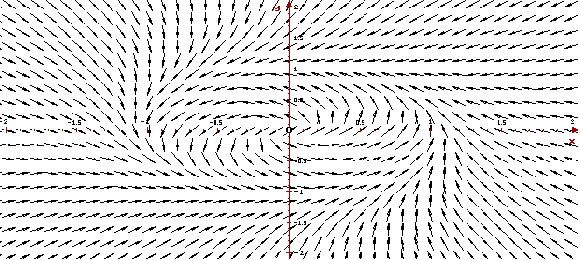
Ниже приведены, построенные программой ОДУ, фазовый портрет и векторное поле системы. На фазовом портрете ясно видно, что фазовые кривые "навиваются" на предельный цикл. Векторное поле показывает направление движения вдоль фазовых кривых с ростом t.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 3. Неустойчивый предельный цикл

Автономная система

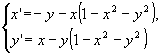
имеет неустойчивый предельный цикл.
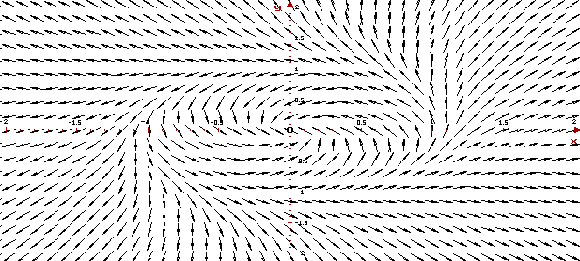
Ниже приведены, построенные программой ОДУ, фазовый портрет и векторное поле системы. На фазовом портрете ясно видно, что фазовые кривые "отходят" от предельного цикла. Векторное поле показывает направление движения вдоль фазовых кривых с ростом t.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 4.  Полуустойчивый предельный цикл

Автономная система

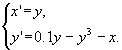
имеет полуустойчивый предельный цикл.
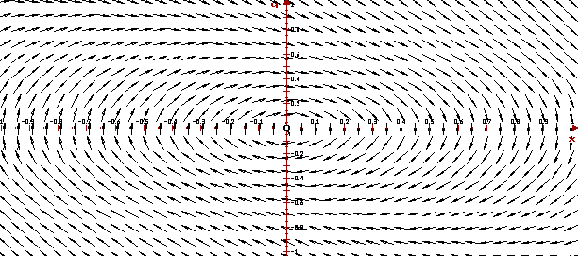
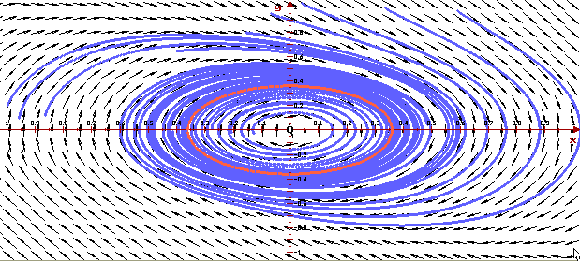
Ниже приведены, построенные программой ОДУ, фазовый портрет и векторное поле системы. На фазовом портрете ясно видно, что фазовые кривые "отходят" от предельного цикла. Векторное поле показывает направление движения вдоль фазовых кривых с ростом t.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica