Вычисление
площадей и длин дуг кривых в декартовых
координатах ~ Вычисление площадей
и длин дуг при параметрическом задании кривых ~
Вычисление площадей и длин дуг
кривых в полярных координатах
Вычисление площадей и длин дуг кривых в
декартовых координатах.
Пусть на плоскости 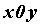 задана область,
ограниченная снизу кривой задана область,
ограниченная снизу кривой 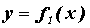 , заданной в
декартовых координатах, сверху – кривой , заданной в
декартовых координатах, сверху – кривой 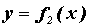 , слева
– прямой , слева
– прямой 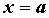 (ее может и не быть, если (ее может и не быть, если 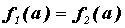 ),
справа – прямой ),
справа – прямой 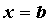 . Исходя из геометрического смысла
определенного интеграла, площадь этой области
можно вычислить по формуле . Исходя из геометрического смысла
определенного интеграла, площадь этой области
можно вычислить по формуле 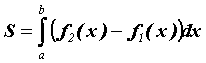 . Здесь не нужно
заботиться, какая из функций и где положительная,
а какая отрицательная. Если, например, . Здесь не нужно
заботиться, какая из функций и где положительная,
а какая отрицательная. Если, например, 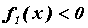 , то
формула сама прибавит нужную площадь. Более
сложные области всегда можно разбить так, чтобы
выполнялись указанные условия. , то
формула сама прибавит нужную площадь. Более
сложные области всегда можно разбить так, чтобы
выполнялись указанные условия.
Пусть на отрезке 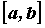 уравнением уравнением 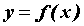 задана
плоская кривая. Ее длина вычисляется по
формуле задана
плоская кривая. Ее длина вычисляется по
формуле 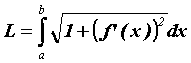
ПРИМЕР 1. Вычисление
площадей и длин дуг в декартовых координатах.
Вычисление площадей и длин дуг при
параметрическом задании кривых.
Если область на плоскости снизу ограничена кривой, заданной
параметрически, то есть 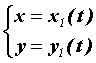 , при этом , при этом 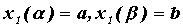 , а
сверху – кривой , а
сверху – кривой 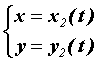 . Тогда площадь такой
плоской фигуры вычисляем по формуле . Тогда площадь такой
плоской фигуры вычисляем по формуле 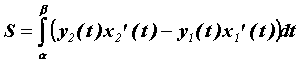 . Эта
формула совпадает с формулой вычисления площади
в декартовых координатах, если учесть, что . Эта
формула совпадает с формулой вычисления площади
в декартовых координатах, если учесть, что 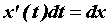 . .
Пусть кривая на плоскости задана
параметрически 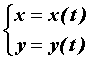 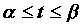 . Тогда длина этой
кривой вычисляется по формуле . Тогда длина этой
кривой вычисляется по формуле 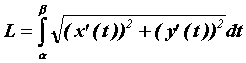 . .
ПРИМЕР 2. Вычисление
площадей и длин дуг при параметрическом задании
кривых.
Вычисление площадей и длин дуг кривых в
полярных координатах.
Когда кривая, ограничивающая область, задана в полярных координатах 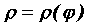 , то
площадь этой области вычисляем по формуле , то
площадь этой области вычисляем по формуле 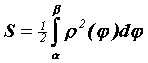 .
Основная трудность в использовании этой формулы
заключается в определении пределов
интегрирования .
Основная трудность в использовании этой формулы
заключается в определении пределов
интегрирования 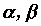 . Здесь нужно
понимать, что кривая . Здесь нужно
понимать, что кривая 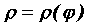 определена только,
если определена только,
если 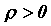 .
Поскольку в формуле присутствует .
Поскольку в формуле присутствует 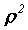 , то она
учтет и не существующую площадь, когда , то она
учтет и не существующую площадь, когда 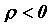 . Решив
уравнение . Решив
уравнение 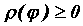 , найдем пределы интегрирования. , найдем пределы интегрирования.
Если кривая, ограничивающая область, задана в
полярных координатах 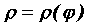 , то ее длина
вычисляется по формуле , то ее длина
вычисляется по формуле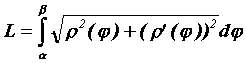 . Пределы
интегрирования определяются из тех же
соображений, что и при вычислении площади. . Пределы
интегрирования определяются из тех же
соображений, что и при вычислении площади.
ПРИМЕР 3. Вычисление
площадей и длин дуг в полярных координатах.

|

