Список встроенных функций

Как описано в предшествующем разделе, Mathcad воспринимает комплексные числа в форме a + bi, где a и b — обычные числа. Можно использовать букву j вместо i, если это удобнее.

Комплексные числа могут также возникать в результате вычислений, даже если все исходные значения вещественны. Например, если вычислить 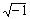, Mathcad вернёт i.

Хотя можно вводить мнимые числа, сопровождая их i или j, Mathcad обычно отображает их сопровождаемыми i. Чтобы Mathcad показывал мнимые числа с j, выберите Формат числа из меню Математика, нажмите на кнопку “Глобальный” и переключите “Мн. ед”. на j.

При вводе комплексных чисел не забудьте, что нельзя использовать i или j сами по себе для ввода комплексной единицы. Нужно всегда печатать 1i или 1j, в противном случае Mathcad истолкует i или j как переменную. Когда курсор покидает выражение, содержащее 1i или 1j, Mathcad скрывает избыточную 1.

Специальные операции над комплексными числами

В Mathcad есть следующие специальные функции и операторы для работы с комплексными числами:

Re(z)	Вещественная часть z.
Im(z)	Мнимая часть z.
arg(z)	Угол в комплексной плоскости между вещественной осью и z. Возвращает результат между -p  и p радиан.
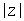	Модуль z. Чтобы записать модуль от выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной полосой | .
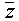	Число, комплексно сопряженное к z. Чтобы применить к выражению оператор сопряжения, выделите выражение, затем нажмите двойную кавычку ("). Число, сопряжённое к a + bi есть a - bi .

Рисунок 2 показывает некоторые примеры использования комплексных чисел в Mathcad.

Рисунок 2: Комплексные числа в Mathcad.

Многозначные функции

При использовании в комплексной области многие функции, о которых мы привыкли думать как о возвращающих одно значение, становятся многозначными.

Общее правило состоит в том, что для многозначной функции Mathcad всегда возвращает значение, составляющее на комплексной плоскости самый маленький положительный угол с положительным направлением действительной оси. Оно называется главным значением.

Например, если требуется вычислить (-1)^1/3 , Mathcad вернёт .5 + .866i , хотя мы обычно считаем -1 кубическим корнем из 1. Дело в том, что .5 + .866i   составляет с положительным направлением вещественной оси угол только в 60 градусов, в то время как -1 составляет 180 градусов.

Единственное исключение из этого правила — оператор n-ого корня, описанный в главе Список операторов. Этот оператор возвращает вещественный корень всякий раз, когда это возможно. Рисунок 3 показывает эту особенность.

Рисунок 3: Нахождение вещественных корней n-ой степени из отрицательного числа.

Список встроенных функций