  Этот
раздел описывает, как вычислять определенные и
неопределенные интегралы, производные и пределы.
Производные
Чтобы вычислить производную в символьном виде,
можно использовать оператор производной Mathcad,
как показано на Рисунке 17:
- Наберите ?, чтобы задать оператор
производной, или [Ctrl]?, чтобы задать
оператор производной более высокого порядка.
- В поле введите выражение, которое требуется
дифференцировать , и переменную, по которой
дифференцируете.
- Нажмите [Shift][F9].

Рисунок 17: Символьное вычисление интегралов и
производных.
Рисунок 18 показывает, как дифференцировать
выражение, не используя оператор производной.
Команда меню Дифференцировать по переменной
дифференцирует выражение относительно
выделенной переменной. Например, чтобы
продифференцировать 2 x2 + y
по x, необходимо: x2 + y
по x, необходимо:
- Выделить x.
- Выбрать команду Дифференцировать по
переменной из меню Символика. Mathcad
отобразит производную, 4
 x. x.
Если выделить переменную y вместо x,
получится ответ 1. Mathcad рассматривает все
переменные, за исключением выделенной, как
константы.
Если не выделить ни x, ни y, команда меню
будет записана серым. Mathcad не может
дифференцировать выражение, потому что
переменная дифференцирования не определена.
Если выражение, в котором выделена переменная,
— элемент массива, Mathcad продифференцирует только
этот элемент массива. Чтобы продифференцировать
весь массив, дифференцируйте каждый элемент по
отдельности, выделяя переменную в каждом
элементе и выбирая команду Дифференцировать по
переменной.
Символьный процессор рассматривает функции,
которых нет в списке встроенных функций, как
неизвестные. При дифференцировании такой
функции символьный процессор будет обычно
выражать ответ в виде операторов производных.
Неопределенные интегралы
В Mathcad есть символьный оператор вычисления
неопределенных интегралов, показанный на
Рисунке 17. Чтобы использовать этот оператор:
- Напечатайте [Ctrl]I, чтобы вставить
оператор неопределенного интеграла и поля ввода
его параметров.
- Заполните поле ввода для подинтегрального
выражения.
- Поместите переменную интегрирования в поле
ввода, следующее за “d”, это может быть имя любой
переменной.
- Заключите выражение в выделяющую рамку.
- Нажмите [Shift][F9].
Рисунок 18 показывает, как интегрировать
выражение, не используя оператор вычисления
неопределенного интеграла. Команда меню Интегрировать
по переменной интегрирует выражение по
выделенной переменной. Например, чтобы
проинтегрировать 2 x2 + y по x,
необходимо: x2 + y по x,
необходимо:
- Выделить x.
- Выбрать пункт Интегрировать по переменной
из меню Символика. Mathcad отобразит результат
интегрирования.
Команда Интегрировать по переменной
интегрирует выражение по выделенной переменной.
Если не выделить переменную, команда меню будет
записана серым. Mathcad не может интегрировать, не
зная переменной интегрирования.
Если символьный процессор не может найти
неопределенный интеграл, он возвращает интеграл
неизменным. Имейте в виду, что многие простые
выражения, например exp(-x3), не
интегрируются в элементарных функциях. Если
результат интегрирования слишком громоздок,
чтобы его отобразить, Mathcad помещает ответ в
текстовой форме в буфере обмена. См. раздел “Длинные ответы”, чтобы
узнать, что делать, когда это случается.
При вычислении неопределенного интеграла
следует помнить, что результат интегрирования
неоднозначен. Если f(x) — интеграл данной
функции, то для любой константы C интегралом
будет также f(x) + C. Таким образом, ответ,
получаемый Mathcad, может отличаться на константу от
ответа, который можно найти в таблицах. Если
продифференцировать функцию и затем
проинтегрировать результат, не обязательно
получится в качестве ответа исходная функция.

Рисунок 18: Дифференцирование и интегрирование
выражений.
Определенные интегралы
Чтобы вычислить символьно определенный
интеграл, надо:
- Напечатать &, чтобы создать оператор
интегрирования с пустыми полями ввода.
- Заполнить поля ввода для пределов
интегрирования. Они могут быть переменными,
константами или выражениями.
- Ввести в поле ввода подинтегральное выражение.
- Заполнить поле ввода позади “d”. Это задаст
переменную интегрирования.
- Окружить всё выражение выделяющей рамкой.
- Нажать [Shift][F9].
Символьный процессор попытается найти
неопределенный интеграл от подинтегрального
выражения перед подстановкой пределов
интегрирования. Если символьный процессор не
сможет найти неопределённый интеграл, появится
соответствующее сообщение об ошибке.
Если символьное интегрирование выполнено
успешно и пределы интегрирования — целые числа,
дроби или точные константы, подобно p , процессор выдаст точное
значение интеграла. Если подинтегральное
выражение или один из пределов содержит
десятичную точку, символьный ответ будет числом,
отображаемым с двадцатью значащими цифрами.
Этот ответ обычно будет совпадать с ответом,
получаемым при численном интегрировании. Однако
символьный и численный ответы получены
совершенно различными путями. Символьный
процессор Mathcad:
- Находит первообразную.
- Вычитает значение первообразной от нижнего
предела интегрирования из значения
первообразной от верхнего предела.
Программа численного интегрирования, с другой
стороны:
- Находит значения подинтегрального выражения во
многих точках на отрезке интегрирования.
- Использует эти значения, чтобы
аппроксимировать интеграл.
Точность этой процедуры интегрирования
зависит от установленного значения переменной TOL
и от гладкости подынтегральной функции.
Конечно, много функций не имеют первообразных,
выражаемых через элементарные функции, и
определенные интегралы, включающие эти функции,
могут быть найдены только численно. Интегралы,
для которых подинтегральное выражение не
является гладкой функцией (имеет разрывы
производной) не могут быть корректно вычислены
символьным процессором.
Пределы
В Mathcad PLUS есть три оператора вычисления
пределов. Они могут быть вычислены только
символьно. Чтобы использовать операторы,
вычисляющие пределы, необходимо:
- Нажать [Ctrl]L, чтобы вызвать оператор
нахождения предела. Чтобы вызвать операторы
нахождения левого и правого пределов, нажмите [Ctrl]B
или [Ctrl]A.
- Введите выражение в поле ввода справа от lim.
- Введите переменную, по которой вычисляется
предел, в левое поле ввода ниже lim.
- Введите значение предела в правое поле ввода
ниже lim.
- Заключите выражение в выделяющую рамку.
- Нажмите [Shift][F9].
Mathcad возвратит результат нахождения предела.
Если предел не существует, Mathcad возвратит
сообщение “неопределено”. Рисунок 19
показывает некоторые примеры вычисления
пределов.
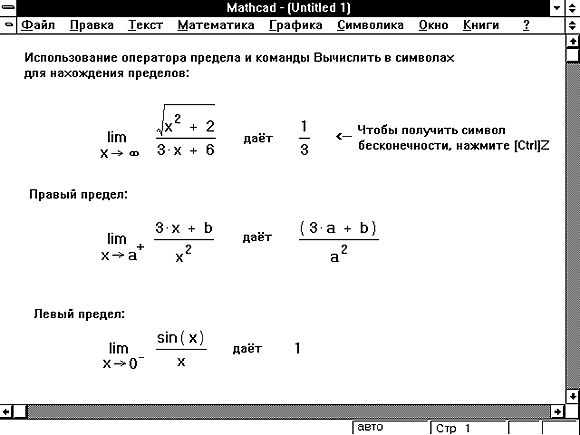
Рисунок 19: Нахождение пределов.
  
|

