  Некоторые
команды из меню Символика позволяют
выполнять алгебраические действия. Можно
упрощать выражения, разлагать их на члены и
сомножители, объединять подобные члены
выражения, находить коэффициенты полиномаhigh,
разлагать выражение в ряд, или изменять все
вхождения переменной на содержимое буфера
обмена.
Символьное преобразование
В общем случае для символьного преобразования
выражения необходимо выполнить следующие шаги:
- Ввести выражение.
- Окружить его синей выделяющей рамкой.
- Нажать [Shift][F9].
В Mathcad PLUS доступны два других способа
преобразовать выражение:
- Можно выбрать Вычислить
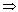 В комплексном виде,
чтобы выразить результаты, когда это возможно, в
комплексной форме. В комплексном виде,
чтобы выразить результаты, когда это возможно, в
комплексной форме.
- Можно выбрать Вычислить
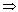 С плавающей запятой,
чтобы выразить, когда это возможно, результат в
числовом виде. С плавающей запятой,
чтобы выразить, когда это возможно, результат в
числовом виде.
При преобразовании выражений, содержащих
комплексные числа, можно выбрать команду Вычислить
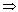 В
комплексном виде из меню Символика. Это
предпишет Mathcad выражать результаты в форме a +
i В
комплексном виде из меню Символика. Это
предпишет Mathcad выражать результаты в форме a +
i b.
Рисунок 8 показывает соответствующий пример. b.
Рисунок 8 показывает соответствующий пример.
Обычно символьный процессор возвращает
результаты, перестраивая переменные. Таким
образом, когда Mathcad преобразует выражение,
содержащее p или e, он
будет обычно возвращать другое выражение,
содержащее p или exp(x).
Чтобы предписать Mathcad возвратить числовые
значения p или e,
выберите Вычислить 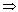 N плавающей запятой
из меню Символика. N плавающей запятой
из меню Символика.
Появится диалоговое окно, в котором можно
определить число цифр справа от десятичной
точки. По умолчанию это число равно 20.

Рисунок 8: Символьное преобразование выражений,
использующее подкоманды, доступные из пункта
меню Вычислить в Mathcad PLUS.
Символьный процессор обрабатывает числа,
содержащие десятичную точку, иначе, чем числа без
десятичной точки. Общее правило следующее:
- Когда символьный процессор получает числа,
содержащие десятичную точку, любые возвращаемые
численные результаты будут десятичными
аппроксимациями точного значения.
- Когда символьный процессор получает числа без
десятичных точек, любые возвращаемые численные
результаты будут выражены без десятичных точек
всякий раз, когда это возможно.
Рисунок 9 показывает некоторые примеры того,
как наличие десятичной точки влияет на ответы,
получаемые от символьного процессора. В этом
примере обратите внимание, что 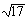 возвращается
неизменённым, так как это число не является
рациональным. Но возвращается
неизменённым, так как это число не является
рациональным. Но 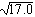 возвращается как десятичная
аппроксимация к иррациональному числу возвращается как десятичная
аппроксимация к иррациональному числу 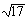 . .
Когда символьная операция дает приближенный
ответ в виде десятичной дроби, этот ответ всегда
отображается с 20 значащими цифрами. На это
отображение не воздействует ни локальный, ни
глобальный числовой формат Mathcad.
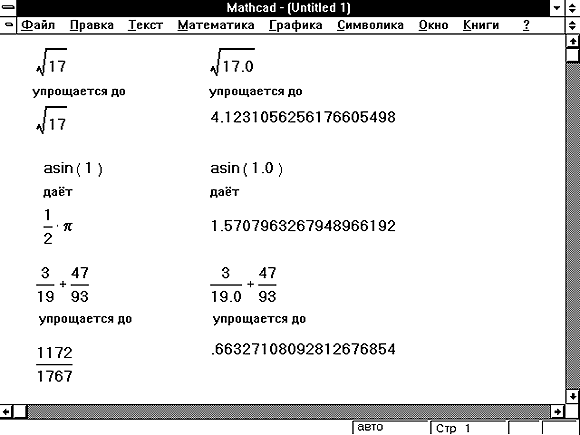
Рисунок 9: Численные ответы в символьных
вычислениях.
Упрощение выражения
Команда Упростить выполняет основные
алгебраическое и тригонометрическое упрощения
выбранного выражения. Упростить выполняет
арифметические преобразования, сокращает общие
множители, использует основные тождества для
тригонометрических и обратных функций, и
упрощает квадратные корни и степени.
Можно упрощать как части выражений (например,
знаменатель дроби, или один член суммы), так и всё
выражение целиком. Можно также упрощать
выражения, содержащие массивы, например, суммы
или произведения матриц. Для этого заключите
требуемую часть выражения в выделяющую рамку
прежде, чем выберете Упростить.
Mathcad иногда может упростить части выражения,
даже если он не может упростить выражение
целиком. Если преобразование всего выражения не
дает желаемый ответ, попытайтесь выделить и
упростить часть выражения. Рисунок 10
иллюстрирует некоторые результаты применения
команды Упростить.
Обычно упрощенный результат тождествен
первоначальному выражению. Однако когда
выражение содержит многолистные функции типа
квадратного корня или обратных
тригонометрических функций, тождество может
нарушаться, что приводит к вычислительным
ошибкам. Например, при упрощении asin(sin(q)) дает q, но это
истинно только когда q —
число между -p/2 и p/2.

Рисунок 10: Некоторые результаты упрощения.
Разложение выражения
Команда Разложить по степеням из меню Символика
разлагает все степени и произведения сумм в
выделенном выражении. Если выражение — дробь,
числитель будет разложен, и выражение будет
представлено как сумма дробей. Синусы, косинусы и
тангенсы сумм переменных, или целого числа,
умноженного на аргумент, будут разложены,
насколько возможно, в выражения, включающие
только синусы и косинусы одиночных переменных.
См. Рисунок 12.
Разложения выражений в ряды
Этот раздел описывает, как использовать
команду Разложить в ряд... ?из меню Символика,
чтобы разложить выражение по формуле Тейлора с
остаточным членом в форме Пеано.
Чтобы использовать команду Разложить в ряд... :
- Выделите переменную в функции или выражении, по
которой требуется найти разложение.
- Выберите Разложить в ряд... . Диалоговое окно
запросит порядок остаточного члена. Это
определит число членов формулы.
Затем Mathcad выдаст соответствующее разложение
выражения по формуле Тейлора. Если выбрать x в
sin(x) и указать порядок остаточного члена 6,
получится разложение функции синус по степеням x,
в котором самая высокая степень x5. Ошибка,
таким образом, имеет порядок О(x6).
Ответы, которые получаются использованием
команды Разложить в ряд... , используют для
остаточного члена обозначение O. Прежде чем
использовать разложение для дальнейших
вычислений, следует удалить этот остаточный
член.
Команда Разложить в ряд... ограничивается
разложением в ряд по одной переменной; любые
другие переменные в выражении обрабатываются
как константы. Mathcad будет искать члены разложения
в ряд Тейлора (ряд по неотрицательным степеням
переменной) для функций, которые являются
аналитическими в 0, и члены разложения в ряд
Лорана для функций, которые имеют полюс
конечного порядка в 0. Чтобы найти члены
разложения в ряд относительно точки, отличной от
0, требуется замена переменной. Например, для
получения членов разложения в ряд для логарифма
в окрестности 1 необходимо:
- Выполнить команду Разложить в ряд... для ln(x
+ 1).
- Использовать Заменить переменную, чтобы
заменить x на x -1.
Рисунок 11 показывает некоторые примеры
разложений, полученных с использованием этой
команды меню. Относительно альтернативного
метода выполнения разложений в ряды см. о
ключевом слове series в разделе “Символьные
преобразования” ранее в этой главе.

Рисунок 11: Разложение в ряд.
При использовании аппроксимаций, полученных с
помощью команды Разложить в ряд... , имейте в
виду следующее:
- Обычно ряд Тейлора функции имеет бесконечное
число членов, в то время как полиномы,
возвращаемые командой Разложить в ряд... ,
имеют только несколько членов (количество членов
зависит от выбранного порядка).
- Ряд Тейлора для функции может сходиться только
в некоторой малой окрестности точки разложения.
Таким образом, когда функция приближается
полиномом, возвращаемым командой Разложить в
ряд... , аппроксимация будет приемлема вблизи
точки разложения, но может быть совершенно
неточной для значений вдали от неё.
Разложение выражения на множители
Команда Разложить на множители... из меню Символика
разлагает на множители выбранное выражение. Если
выражение представляет целое число, Mathcad
разложит его на множители по степеням простых
чисел. В остальных случаях Mathcad будет пытаться
преобразовывать выражение в произведение. Эта
команда будет объединять сумму дробей в одну
дробь и будет упрощать многоэтажную дробь с
несколькими дробными чертами.
Обратите внимание, что при использовании этой
команды Mathcad разлагает на множители “только то,
что выделено”. Например, если выделить всё
выражение
a b + a b + a c + x c + x
и выбрать команду Разложить на множители... ,
Mathcad вернёт это выражение неизменённым, потому
что выбранное выражение целиком не факторизуемо.
Но если выбрать только первые два члена, Mathcad
возвратит
a (b + c) + x (b + c) + x
Разлагая на множители, всегда можно немного
упростить выражение, выбирая и разлагая на
множители подвыражения, даже если выражение в
целом не факторизуемо. Команду Разложить на
множители... следует использовать также, чтобы
объединить сумму дробей в одну дробь или
упростить сложную дробь. См. примеры на Рисунке 12.
Поскольку выделяющая рамка следует структуре
выражения, может понадобиться прежде вставить
скобки, чтобы удалось выделить требуемое
подвыражение. Например, чтобы выделить a c + x
в выражении, приведенном выше, необходимо
вставить левую скобку перед вторым a и правую
скобку — после x. c + x
в выражении, приведенном выше, необходимо
вставить левую скобку перед вторым a и правую
скобку — после x.
Приведение подобных членов
Команда меню Разложить по подвыражению...
объединяет члены, содержащие одинаковые степени
выделенного подвыражения. Результатом является
полином от подвыражения. Выбираемое
подвыражение должно быть либо простой
переменной, либо встроенной функцией вместе с
аргументом. См. пример на Рисунке 12.

Рисунок 12: Разложение по степеням, разложение
на множители и приведение подобных членов.
Разложение на элементарные дроби
Чтобы преобразовать выражение в сумму
элементарных дробей:
- Выделите переменную в знаменателе выражения.
- Выберите Разложить на элементарные дроби из
меню Символика.
Символьный процессор будет пытаться разлагать
знаменатель выражения на линейные или
квадратичные множители, имеющие целочисленные
коэффициенты. Если это удастся, он будет
разлагать выражение в сумму дробей с этими
множителями в качестве знаменателя. Все
константы в выделенном выражении должны быть
целыми числами или дробями: Mathcad не будет
разлагать выражение, которое содержит
десятичные точки. См. некоторые примеры на
Рисунке 13.

Рисунок 13: Разложение на элементарные дроби.

Рисунок 14: Нахождение коэффициентов
некоторых полиномов.
Нахождение коэффициентов полинома
Многие выражения могут быть перезаписаны в
виде полиномов от выделенной переменной или
относительно подвыражения. В Mathcad PLUS для этого
можно использовать символьный процессор:
- Выделив переменную, относительно которой
требуется разложить выражение в полином.
- Выбрав Полиномиальные коэффициенты из меню Символика.
Mathcad возвращает вектор, содержащий
коэффициенты требуемого полинома в порядке
возрастания степеней. Первое выражение на
Рисунке 14 показывает пример такой операции.
Если нужно, чтобы символьнай процессор
рассматривал выражение как полином относительно
функции, заключите в выделяющую рамку функцию.
Второе выражение на Рисунке 14 показывает пример
разложения по степеням sin(x).
Замена переменных
Эта команда заменяет выделенным выражением
заданную переменную. Чтобы использовать эту
команду:
- Выделите выражение, которое будет заменять
переменную.
- Скопируйте его в буфер обмена, выбирая команду
Копировать из меню Правка.
- Выделите переменную, которую нужно заменить, и
выберите Заменить переменную из меню Символика.
Mathcad подставит выражение из буфера обмена
вместо выделенной переменной. Если переменная
появляется более чем один раз в преобразуемом
выражении, Mathcad заменит все её вхождения на
содержимое буфера обмена. Рисунок 15 показывает
некоторые примеры.
Обратите внимание, что команда Заменить
переменную не может подставлять векторы или
матрицы. Чтобы подставить скалярное выражение
вместо переменной, которая находится в матрице,
поместите выражение в буфер обмена, используя
команду Копировать. Затем щёлкните кнопкой
мыши на каждом элементе матрицы, который
содержит заменяемую переменную, и выберите Заменить
переменную.

Рисунок 15: Замена переменной выражением.
Вычисление сумм
Чтобы вычислить сумму в символьном виде, можно
использовать оператор суммирования Mathcad:
- Вызовите оператор суммирования, печатая [Ctrl][Shift]4.
- Введите выражение, которое нужно суммировать, в
месте ввода справа от “
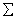 “. “.
- Поместите индекс и диапазон суммирования в поля
выше и ниже “
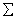 “, как показано на Рисунке 16. “, как показано на Рисунке 16.
- Окружите всё выражение выделяющей рамкой и
нажмите [Shift][F9].
Вычисление произведения по индексу
производится аналогично, за исключением того,
что требуется напечатать [Ctrl][Shift]3, чтобы
получить оператор произведения. Если при
суммировании или вычислении произведения
используются числовые пределы, убедитесь, чтобы
верхний предел был больше или равен нижнему.
Обратите внимание, что, как и при всех
символьных операциях, символьный процессор не
знает ничего относительно любых определений
переменных в рабочем документе. Таким образом,
если определить 10-мерный вектор v, символьное
суммирование по диапазону от i =, 0 . . 9 даст только
формальную сумму v0 + v1 +...+v9. Если
нужно получить числовой ответ, используйте
операторы суммы и произведения.
Вычисление других функций и операторов
Как правило, можно символьно преобразовать
любую комбинацию встроенных функций Mathcad. Если
результат может быть вычислен точно — sin(p), например, — появится точный ответ.
В противном случае Mathcad будет возвращать в
качестве ответа первоначальное выражение.
Рисунок 16 иллюстрирует различные результаты
символьного вычисления.

Рисунок 16: Символьное вычисление сумм,
произведений и функций.
  
|

