Синтаксис:

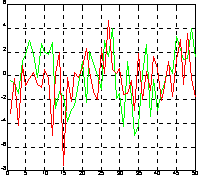
Описание:

Функция Y = fft2(X) вычисляет для массива данных X двумерное дискретное преобразование Фурье. Если массив X двумерный, вычисляется дискретное преобразование для каждого столбца.

Функция Y = fft(X, n) вычисляет n-точечное дискретное преобразование Фурье. Если length(X) < n, то недостающие строки массива X заполняются нулями; если length(X) > n, то лишние строки удаляются.

Функция X = ifft(Y) вычисляет обратное преобразование Фурье для массива Y.

Функция X = ifft(Y, n) вычисляет n-точечное обратное преобразование Фурье для массива Y.

Примеры:

Рассмотрим тот же пример, что и для функции fft, но сформируем 2 входных последовательности (рис. а):

             t = 0:0.001:0.6;
             x = sin(2*pi*50*t) + sin(2*pi*120*t);
             y1 = x + 2*randn(size(t));
             y2 = x + 2*randn(size(t));
             y = [y1; y2];
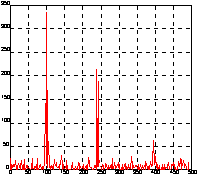
             plot(y(1, 1:50)), hold on, plot(y(2, 1:50)), grid, hold off

Применим двумерное преобразование Фурье для сигнала y на основе 512 точек и построим график спектральной плотности. Теперь можно выделить 2 частоты, на которых амплитуда спектра максимальна. Это частоты - 100/2Гц и 240/2Гц.

             Y = fft2(y, 2, 512);
             Pyy = Y.*conj(Y)/512;
             f = 1000*(0:255)/512;
             figure(2), plot(f, Pyy(1:256)), grid

а)	б)

Алгоритм:

Двумерное дискретное преобразование связано с одномерным дискретным преобразованием Фурье следующим образом:

               fft2(X) = fft(fft(X).’).’

Сопутствующие функции: FFT, IFFT, FFTSHIFT, Signal Processing Toolbox.

Ссылки:

1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.