  Можно
использовать Mathcad для отображения функций,
которые неудобно воспроизводить в декартовых
координах. Например, легко можно было бы
нарисовать диаграмму направленности
радиоантенны или интенсивность электрического
поля вокруг объекта.
Чтобы создать график в полярных координатах:
- Щёлкните мышью там, где нужно создать график.
- Выберите Полярный график из меню Графика.
Mathcad показывает круг с четырьмя полями ввода, как
показано на Рисунке 1.
- Выше области графика определите угол q и функцию угла r(q).
- Поле ввода внизу предназначено для угловой
переменной графика. Введите туда дискретную
переменную или любое выражение, включающее
дискретную переменную.
- Поле ввода слева должно содержать выражение для
радиуса.
- Два поля ввода справа предназначены для
верхнего и нижнего граничных значений радиуса.
Mathcad заполняет эти поля по умолчанию.
Если требуется, можно изменять эти
пределы. См. раздел “Форматирование
осей” .
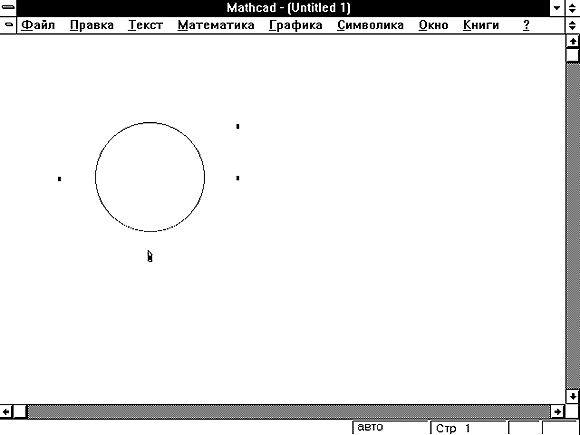
Рисунок 1: Пустые поля ввода в области
полярного графика.
Как и в случае с выражением, Mathcad не
обрабатывает график, пока Вы или не нажмете [F9],
или, в автоматическом режиме, не щёлкните мышью
вне области графика.
В Mathcad полярные графики рисуются путем замены r
и q на декартовы координаты
x и y с использованием стандартных
преобразований x = r cos(q)
и y = r sin(q).
Предполагается, что r и q
могут принимать и положительные, и
отрицательные значения.
Можно определять многие из характеристик
полярного графика, включая размер, число линий
сетки и верхнее и нижнее граничные значения по
радиальной оси. Процедуры для определения этих
характеристик описаны ниже в этой главе.
Типичный полярный график показывает
зависимость выражения для радиуса от выражения
для угла. Чтобы увидеть такой график, нужно
сначала определить функцию, затем создать её
полярный график. Ниже приведена типичная
последовательность создания графика функции,
подобной показанной на Рисунке 2:
- Определите приращение для q.
- Определите q как
дискретный аргумент с заданным приращением.
- Определите r(q) как
функцию q.
- Отобразите график r(q) в
полярных координатах.
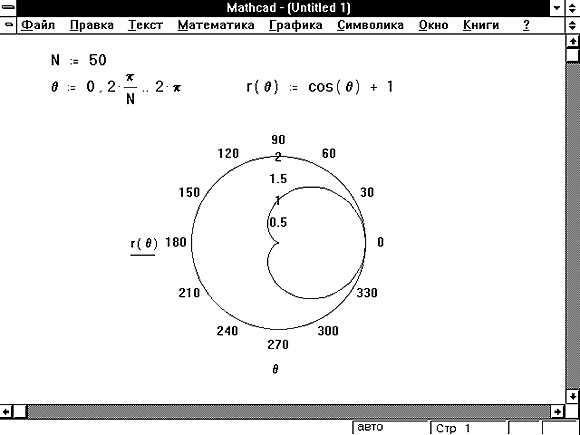
Рисунок 2: Полярный график функции от q.
  
|

