|
§ 1. Определения свободного и закрепленного
геометрических векторов.
Определение 1: Закрепленный вектор – отрезок с упорядоченными концами: AB,
A – начало вектора, В – конец вектора, АВ ≠ ВА.Конец и начало вектора могут совпадать: АА –
нулевой вектор.
Определение 2: Равенство закрепленных векторов:
Пусть AB и CD – закрепленные ненулевые векторы.
1) Соединим А с С и В с D (начальные и конечные точки векторов).
Если ABDC – параллелограмм, то AB = CD.2) AB = CD, если
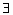 закрепленный вектор EF : AB = EF и EF = CD. закрепленный вектор EF : AB = EF и EF = CD.
3) Все нулевые векторы равны: АА = ВВ.
Определение 3: Свободный вектор (или просто
вектор) – множество равных между собой (в смысле определения 2) закрепленных векторов.
Свободные векторы обозначаются прописными латинскими буквами – a.
Нулевой свободный вектор обозначается θ.
Определение 4:
Закрепленный вектор AB является реализацией свободного вектора a,
если a = { CD : CD = AB } ( То есть свободный вектор a – это множество закрепленных векторов CD,
т.ч. CD = AB. )
Обозначение: AB 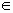 a (допустимо а = АВ).
a (допустимо а = АВ).
Предложение 1.  с.в.
а и с.в.
а и  т. О пространства т. О пространства 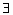 ! з.в. ОА : ОА
! з.в. ОА : ОА 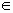 а. а.
( Т.е. для любого свободного вектора a и для любой точки О пространства существует
единственный закреплённый вектор OA, который является реализацией а. )
Определение 5: Длина свободного вектора
a
– это длина его реализации:
|a| = |AB|, если AB 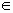 a, |θ| = 0. a, |θ| = 0.
Определение 6: Угол между свободными векторами а и b
– это наименьший угол между их реализациями ОА и ОВ ( ОА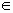 а,
ОВ а,
ОВ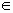 b ). b ).
Определение 7: Свободные векторы a и b равны
(a = b), если они совпадают как множества.
Из определения свободного вектора очевидно, что для того, чтобы задать свободный вектор a, достаточно задать
какую-либо его реализацию, т.е. закрепленный вектор AB 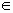 a. a.
Определение 8: V3 – множество всех свободных векторов в пространстве R3.


|

