  Символьный
процессор Mathcad рассматривает функции и
переменные не совсем так, как числовой процессор.
Эти различия связаны с ответом на следующий
вопрос:
- Знает ли символьный процессор, что функция или
переменная определена в другом месте?
Ответ на этот вопрос зависит от двух вещей:
- Является ли функция или переменная встроенной,
или определяется где-нибудь в рабочем документе?
- Используются ли символьный знак равенства или
команды меню?
Следующие два раздела описывают, что Mathcad
делает с переменными и функциями при символьных
преобразованиях.
И ещё одно замечание. Символьные
преобразования могут иногда возвращать функции
и константы, которые не существуют в списке
встроенных функций и констант Mathcad. Они описаны в
последнем подразделе “Специальные
функции”.
Встроенные функции и переменные
Вообще говоря, символьный и численный
процессоры Mathcad используют несовпадающие списки
функций. Эти списки частично пересекаются: часть
встроенных функций (тех функций, которые
вычисляются численным процессором), имеющих
общепринятое математическое значение подобно sin
и log, участвуют в символьных преобразованиях.
Другие функции, подобно linterp или rnd, не
имеющие общепринятого математического значения,
не преобразуются символьным процессором. С
другой стороны, символьный процессор использует
ряд функций, не вычисляемых численным
процессором. Список таких функций приведён в
подразделе “Специальные функции”.
Список встроенных функций, используемых в
символьных вычислениях включает:
тригонометрические и гиперболические функции и
обратные им; логарифмические и показательные
функции; функции Re и Im; функцию erf;
функцию Г; функцию mod; Ф (ступенчатая
функция Хэвисайда); max и min; матричные
функции identity и eigenvalseigenvalues. В целом эти
функции трактуются одинаково символьным и
численным процессорами. Имеется три небольших
различия:
- В отличие от численной функции mod символьная
функция mod требует целочисленный аргумент и
может принимать полиномы в качестве первого
аргумента (см. Рисунок 16).
- Некоторые обратные тригонометрические функции
используют различные ветви на комплексной
плоскости.
- Функция eigenvals будет работать в
символьном виде как для комплексных, так и для
вещественных матриц; численно eigenvals вычисляется
только для вещественных матриц.
Если встроенные константы имеют общепринятое
математическое значение, они также трактуются
одинаково как символьным, так и численным
процессорами. Символьный процессор распознаёт p , e и 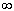 . Они сохраняют свой
точный смысл при использовании в символьном
виде. . Они сохраняют свой
точный смысл при использовании в символьном
виде.
При символьных преобразованиях нет никакой
необходимости использовать приближение 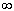 как 10307
или ограничивать p только
пятнадцатью значащими цифрами. как 10307
или ограничивать p только
пятнадцатью значащими цифрами.
Встроенные константы, не имеющие общепринятого
математического значения, не распознаются
символьным процессором. Например, TOL и ORIGIN
не будут иметь свои обычные значения в
символьных преобразованиях. Они будут
обрабатываться подобно любой другой
неопределенной переменной.
Рисунок 28 показывает различие в способах,
которыми Mathcad обрабатывает функции в символьных
преобразованиях. Обратите внимание, что
символьный процессор распознает и вычисляет
функцию sin, но когда запрашивается вычисление
rnd(3), символьный процессор просто возвращает
rnd(3).

Рисунок 28: Некоторые функции воспринимаются
символьным процессором, в то время как другие —
нет.
Функции и переменные, определяемые
пользователем
Функции и переменные, которые Вы определяете
самостоятельно, распознаются символьным
процессором при использовании символьного знака
равенства, обсужденного в разделе “Символьные преобразования” этой
главы. Однако они не распознаются при
использовании команд меню. Рисунок 29 показывает
это различие.

Рисунок 29: Функции и переменные, определяемые
пользователем распознаются только при
использовании символьного знака равенства.
Специальные функции
Результат символьного преобразования иногда
содержит функции, которые не является частью
списка встроенных функций Mathcad. Перечень,
приведенный ниже, дает определения специальных
функций. Определения всех функций, кроме Ei, erf
и Zeta, являющихся суммами рядов, и W,
можно использовать, чтобы вычислить численные
значения.
|
g —
константа Эйлера, приблизительно равная 0.5772156649. |
|
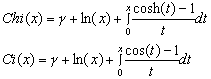 |
|
csgn(z) = 1, если Re(z) > 0 или (Re(z) > 0 и
Im(z) 0); в
остальных случаях. Определяется в Mathcad как: 0); в
остальных случаях. Определяется в Mathcad как:
if(Re(x) 0,
2Ф(Re(x)) - 1, 2Ф(Im(x)) - 1) 0,
2Ф(Re(x)) - 1, 2Ф(Im(x)) - 1) |
|
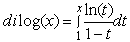 |
|
Dirac(x) = 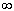 , если x = 0 и 0 в
остальных случаях. , если x = 0 и 0 в
остальных случаях. |
|
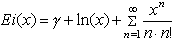 (x > 0) (x > 0) |
|
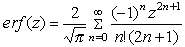 (для комплексного z) (для комплексного z) |
|
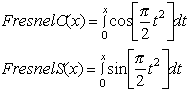 |
|
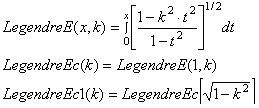 |
|
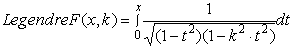 |
|
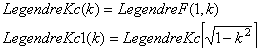 |
|
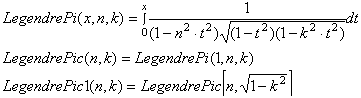 |
|
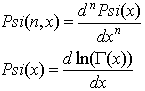 |
|
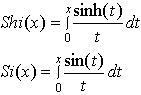 |
|
signum(x) = 1 , если x = 0, в противном
случае вычисляется в Mathcad как (x = 0) +x/|x| |
|
W(x) = главная ветвь функции,
удовлетворяющей условию W(x) exp(W(x)) = x. exp(W(x)) = x. |
|
W( n, x) = n-ная ветвь W (x). |
|
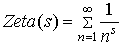 (s>1) (s>1) |
Функции arcsec, arccsc, arccot, arcsech,
arcscsh, arccoth могут быть вычислены заменой
аргумента и использованием встроенных в Mathcad
функций acos, asin, и т.д. Например:
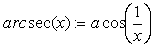
Функции Psi и Г-функция Эйлера появляются
часто в результате вычисления бесконечных сумм и
произведений. Чтобы вычислить сумму ряда или
бесконечное произведение, необходимо поместить
символ 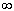 в поле верхнего предела оператора суммы
(произведения).
в поле верхнего предела оператора суммы
(произведения).
  
|

