Обусловленность
вычислительной задачи ~ Число
обусловленности ~ Обусловленность
задачи нахождения корня ~ Интервал
неопределенности корня ~ Применение
метода Ньютона для нахождения кратного корня
Под обусловленностью вычислительной
задачи понимают чувствительность ее решения к
малым погрешностям входных данных.
Пусть установлено неравенство 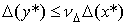 ,
где ,
где 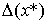 - относительная
погрешность входных данных, а - относительная
погрешность входных данных, а 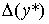 -
относительная погрешность решения. Тогда -
относительная погрешность решения. Тогда 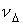 -
называется абсолютным числом обусловленности
задачи. Если же установлено неравенство -
называется абсолютным числом обусловленности
задачи. Если же установлено неравенство 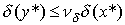 между
относительными погрешностями данных и решения,
то между
относительными погрешностями данных и решения,
то 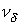 называют относительным числом
обусловленности задачи. называют относительным числом
обусловленности задачи.
Обычно под числом обусловленности 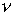 понимают
относительное число обусловленности. Если понимают
относительное число обусловленности. Если 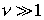 ,
то задачу называют плохо обусловленной. ,
то задачу называют плохо обусловленной.
Обусловленность задачи нахождения
корня. Пусть 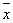 v корень, подлежащий
определению. Будем считать, что входными данными
для задачи вычисления корня являются значения
функции v корень, подлежащий
определению. Будем считать, что входными данными
для задачи вычисления корня являются значения
функции 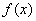 . Так как . Так как 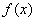 v
вычисляется приближенно, то обозначим функцию,
полученную в действительности через v
вычисляется приближенно, то обозначим функцию,
полученную в действительности через 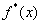 .
Предположим, что в малой окрестности корня
выполняется неравенство: .
Предположим, что в малой окрестности корня
выполняется неравенство: 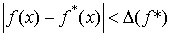 . Для
близких к . Для
близких к 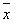 значений значений 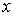 справедливо равенство
справедливо равенство 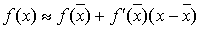 ,
следовательно, ,
следовательно, 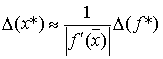 . Это означает, что число
обусловленности задачи нахождения корня равно . Это означает, что число
обусловленности задачи нахождения корня равно 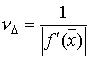 . Из последней формулы
следует, что чем меньше значение производной
функции в точке корня, тем задача хуже
обусловлена. В частности, задача нахождения
кратного корня имеет число обусловленности -
бесконечность. . Из последней формулы
следует, что чем меньше значение производной
функции в точке корня, тем задача хуже
обусловлена. В частности, задача нахождения
кратного корня имеет число обусловленности -
бесконечность.
Интервал неопределенности корня.
Если функция 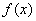 непрерывна, то найдется такая
малая окрестность непрерывна, то найдется такая
малая окрестность 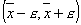 корня корня 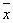 , имеющая
радиус , имеющая
радиус 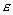 , в которой выполнено неравенство , в которой выполнено неравенство 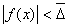 .
Это означает, что .
Это означает, что 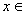 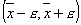 знак
вычисленного значения знак
вычисленного значения 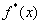 , вообще
говоря не обязан совпадать со знаком , вообще
говоря не обязан совпадать со знаком 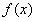 и,
следовательно, становится невозможным
определить, какое именно значение и,
следовательно, становится невозможным
определить, какое именно значение 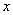 из
интервала из
интервала 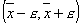 обращает функцию обращает функцию 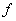 в нуль. Этот
интервал называется интервалом
неопределенности корня. Очевидно, что радиус
интервала неопределенности для простого корня
равен в нуль. Этот
интервал называется интервалом
неопределенности корня. Очевидно, что радиус
интервала неопределенности для простого корня
равен 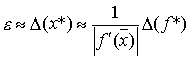 . Аналогично можно показать, что
для кратного корня . Аналогично можно показать, что
для кратного корня 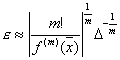 . Это означает, что для
простого корня радиус интервала
неопределенности прямо пропорционален
погрешности вычисления функции . Это означает, что для
простого корня радиус интервала
неопределенности прямо пропорционален
погрешности вычисления функции 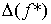 , а для
кратного корня , а для
кратного корня 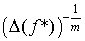 . .

ПРИМЕР 1. Теоретическая
оценка радиуса интервала неопределенности
корня.
Пусть 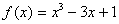 . Корень уравнения простой и равен . Корень уравнения простой и равен 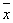 =
-0.34729635533861. Тогда =
-0.34729635533861. Тогда 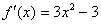 и и 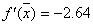 . Если . Если 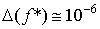 ,
то ,
то 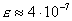 . Это означает , что найти корень с
точностью меньшей, чем радиус интервала
неопределенности, не удастся. . Это означает , что найти корень с
точностью меньшей, чем радиус интервала
неопределенности, не удастся.

ПРИМЕР 2. Вычислительный
эксперимент по нахождению интервала
неопределенности корня.
Применение метода Ньютона для
нахождения кратного корня. Метод Ньютона для
случая кратного корня обладает лишь линейной
скоростью сходимости. Чтобы сохранить
квадратичную сходимость его модифицируют
следующим образом:
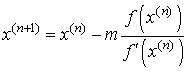 , где , где 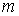 - кратность корня. - кратность корня.
Как правило, значение 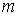 v
неизвестно. Используя метод Ньютона, можно
узнать кратность корня. Для этого будем задавать
значения v
неизвестно. Используя метод Ньютона, можно
узнать кратность корня. Для этого будем задавать
значения 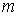 = 1,2,3 и вычислять значение корня с
заданной точностью , одновременно подсчитывая
количество итераций для каждого значения = 1,2,3 и вычислять значение корня с
заданной точностью , одновременно подсчитывая
количество итераций для каждого значения 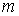 .
При некотором значении .
При некотором значении 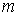 число
итераций будет минимальным. Это значение число
итераций будет минимальным. Это значение 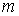 и
есть кратность корня. и
есть кратность корня.
ПРИМЕР 3. Определение
кратности корня методом Ньютона.

|

