Зависимые случайные величины ~ Условная плотность распределения ~ Нормальное распределение

Зависимые случайные величины

Если две случайные величины x и h зависимы, то информация о том, какое значение приняла одна из них меняет наше представление о распределении другой.

Иначе говоря, по распределению двумерной случайной величины (x , h ) можно судить о распределении каждой из величин x и h .

В случае непрерывных двумерных случайных величин условные распределения строятся по следующей схеме.

Если p_{(x , h )}(x, y) - плотность вероятностей совместного распределения двумерной случайной величины (x , h ), то плотности вероятностей каждой ее компоненты вычисляются по формулам:

, .

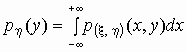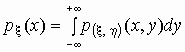Условной плотностью распределения случайной величины x при условии, что случайная величина h принимает значение h = y₀, называется функция переменной x, определяемая формулой

.

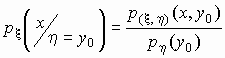Аналогично, условной плотностью распределения случайной величины h при условии, что случайная величина x принимает значение x = x₀, называется функция переменной y, определяемая формулой

.

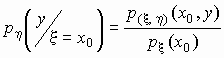ПРИМЕР 1. Независимость компонент непрерывного случайного вектора

Рассмотрим пример непрерывной двумерной случайной величины, распределенной равномерно в единичном круге. Найдем плотности вероятностей каждой компоненты и их условные плотности вероятностей. Проверим независимость компонент двумерной случайной величины.

Нормальное распределение

Важный для дальнейшего пример дает случайный вектор (x , h ), имеющий нормальное распределение.

В наиболее общем случае плотность вероятностей такого вектора зависит от пяти параметров a_x , a_h , s _x , s _h и k_{x h} и имеет вид:

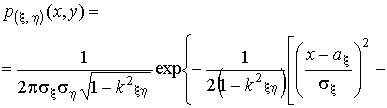
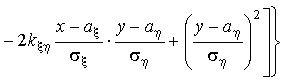
При любых значениях параметров a_x , a_h , s _x , s _h , k_{x h} | k_{x h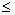}| 1 эта функция удовлетворяет условиям нормировки:

.

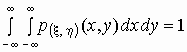Кроме того, можно легко найти плотность распределения каждой из случайных величин x и h :

,

,

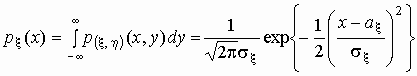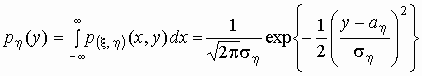т.е. случайные величины x и h имеют нормальные распределения с параметрами a_x , a_h , s _x >0,

s _h >0: N(a_x , s _x ), N(a_h , s _h ).

Рассмотрим теперь условное распределение x при условии h = y. Для этого, выполнив несложные вычисления, найдем

.

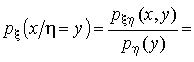
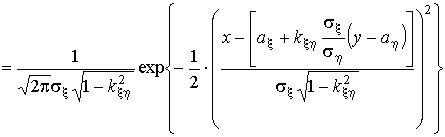Это нормальное распределение с параметрам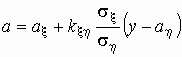и и .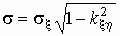

Аналогично можно найти условное распределение условное распределение h при условии x = x:

,

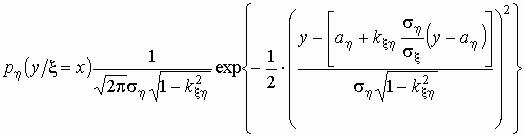Видно, что оно тоже является нормальным с параметрам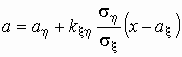и и .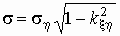

ПРИМЕР 2. Независимость компонент нормально распределенного случайного вектора

Рассмотрим пример непрерывной двумерной случайной величины, распределенной нормально с параметрами a_x =0, a_h =1, s _x =1, s _h=2 , k_{x h}=0.5.  Найдем плотности вероятностей каждой компоненты и их условные плотности вероятностей. Проверим независимость компонент двумерной случайной величины.