Определение независимых величин ~ Независимые непрерывные величины ~ Независимые дискретные величины

Определение независимых величин

По известному совместному распределению двумерной случайной величины нетрудно найти распределения его компонент. Решить обратную задачу, т.е. восстановить совместное распределение (x , h ) по известным распределениям величин x и h , вообще говоря, невозможно. Однако эту задачу можно решить, когда случайные величины x и h н е з а в и с и м ы.

Случайные величины называются независимыми, если для любых x₁, x₂ R²

.

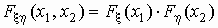
Независимые непрерывные величины

Для непрерывных случайных величин это определение эквивалентно такому:

случайные величины называются независимыми, если

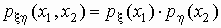
во всех точках непрерывности входящих в это равенство функций.

ПРИМЕР 1. Найдем распределение компонент непрерывного двумерного случайного вектора и проверим их независимость.

Независимые дискретные величины

Для дискретных случайных величин x и h с матрицей совместного распределения {p_ij} условие независимости x и h имеет вид:

,

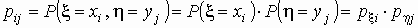для всех i = 1, 2, …, n; j = 1, 2, …, m.

В частности, случайные величины x и h , заданные совместным распределением

зависимы, поскольку p₁₁ = 0.1, а p_{x 1}p_{h 1} = (0.1+0.1)*(0.1+0.1+0.2) = 0.2*0.4 = 0.08.

В то же время в совместном распределении x и h

величины x и h н е з а в и с и м ы.

ПРИМЕР 2. Найдем распределение компонент дискретного двумерного случайного вектора и проверим их независимость.