Равномерное
распределение ~ Экспоненциальное
(показательное) распределение ~ Нормальное
распределение ~ Распределение
хи-квадрат (c 2-
распределение) ~ F-распределение
Фишера ~ Распределение Парето ~ Логистическое распределение ~ Логнормальное распределение ~ Вета-распределение ~ Распределение
Вейбулла ~ Распределение Коши ~ Гамма-распределение ~ Распределение
Лапласа
Равномерное распределение
Непрерывная случайная величина x
, принимающая значения на отрезке [a, b],
распределена равномерно на [a, b], если ее
плотность распределения px (x)
и функция распределения Fx (x ) имеют
соответственно вид:
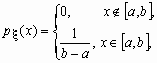 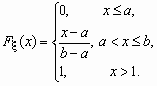 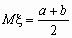 , , 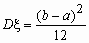 . .
Экспоненциальное (показательное)
распределение
Непрерывная случайная величина x имеет показательное распределение с
параметром l > 0, если она
принимает только неотрицательные значения, а ее
плотность распределения px (x
)и функция распределения Fx (x)
имеют соответственно вид:
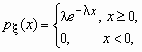 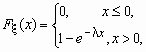 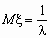 , , 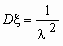 . .
Нормальное распределение
Нормальное распределение играет
исключительно важную роль в теории вероятностей
и математической статистике.
Случайная величина x нормально
распределена с параметрами a и s
, s >0, если ее плотность
распределения px (x ) и
функция распределения Fx (x)
имеют соответственно вид:
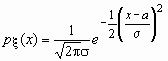 , , 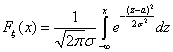 , Mx = a, Dx = s 2. , Mx = a, Dx = s 2.
Часто используемая запись x ~
N(a, s ) означает, что случайная
величина x имеет нормальное
распределение с параметрами a и s
.
Говорят, что случайная величина x
имеет стандартное нормальное распределение,
если a = 0 и s = 1 (x ~
N(0, 1)). Плотность и функция распределения
стандартного нормального распределения имеют
вид:
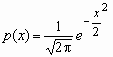 , , 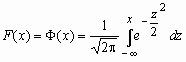 , Mx = 0, Dx = 1. , Mx = 0, Dx = 1.
Здесь 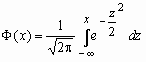 - функция
Лапласа. - функция
Лапласа.
Функция распределения нормальной величины x ~ N(a, s )
выражается через функцию Лапласа следующим
образом: 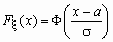 . .
Если x ~ N(a, s
), то случайную величину h = (x-a)/s называют стандартизованной или
нормированной случайной величиной; h
~ N(0, 1) - имеет стандартное нормальное
распределение.
Распределение хи-квадрат (c
2- распределение)
Пусть x 1, x 2,
…, x n - независимые
случайные величины, каждая из которых имеет
стандартное нормальное распределение N(0, 1).
Составим случайную величину
c 2 = x 12
+ x 22 + …+ x
n2.
Ее закон распределения называется c
2- распределением с nстепенями свободы.
Плотность вероятности этой случайной величины
вычисляется по формуле:
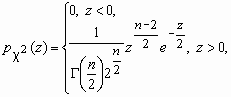 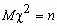 , Dc 2=2n. , Dc 2=2n.
Здесь 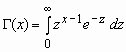 -
гамма-функция Эйлера. -
гамма-функция Эйлера.
Распределение Стьюдента
Пусть случайная величина x
имеет стандартное нормальное распределение, а
случайная величина c n2
- c 2-распределение с n
степенями свободы. Если x и c n2 - независимы, то про
случайную величину 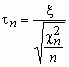 говорят, что она имеет распределение
Стьюдента с nстепенями свободы. Плотность
вероятности этой случайной величины вычисляется
по формуле: говорят, что она имеет распределение
Стьюдента с nстепенями свободы. Плотность
вероятности этой случайной величины вычисляется
по формуле:
 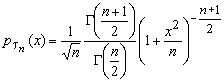 , x , x  R,
Mt n = 0, Dt n = n/(n-2), n>2. R,
Mt n = 0, Dt n = n/(n-2), n>2.
При больших n распределение Стьюдента
практически не отличается от N(0, 1).
F-распределение Фишера
Пусть случайные величины c n2и
c m2 независимы и
имеют распределение c 2 с n
и mстепенями свободы соответственно. Тогда о
случайной величине 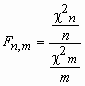 говорят,
что она имеет F-распределение. Плотность
вероятности этой случайной величины вычисляется
по формуле: говорят,
что она имеет F-распределение. Плотность
вероятности этой случайной величины вычисляется
по формуле:
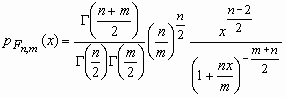 , x>0, , x>0, 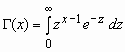 - -
гамма-функция
Эйлера; 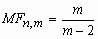 ,
m>2; ,
m>2; 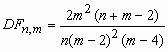 , m
> 4. , m
> 4.
Распределение Парето
Распределение Парето часто применяется в
экономических исследованиях. Плотность
вероятностей для случайной величины,
распределенной по Парето, имеет вид
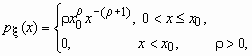 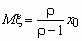 , , 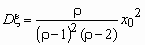 . .
Распределение Парето имеет математическое
ожидание только при r > 1, а
дисперсию - только при r > 2.
Cлучайная величина, распределенная по Парето,
принимает значения только в области x 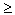 x0, x0
> 0. x0, x0
> 0.
Логистическое распределение
Это еще одно распределение, широко
применяемое в экономических исследованиях. Для
случайной величины x , имеющей
логистическое распределение, функция
распределения и функция плотности вероятностей
имеют соответственно вид:
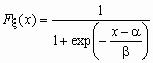 , , 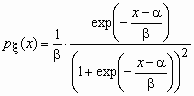 , ,
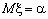 , , 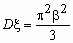 , x , x  R,
a и b - параметры
распределения. R,
a и b - параметры
распределения.
По своим свойствам логистическое
распределение очень похоже на нормальное.
Логнормальное распределение
Случайная величина x имеет
логарифмическое нормальное (логнормальное)
распределение с параметрами a и s
, если случайная величина lnx имеет
нормальное распределение с параметрами a >и s . Функция распределения и функция
плотности вероятностей логнормального
распределения имеют соответственно вид:
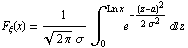 , , 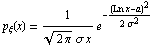 , , 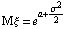 , , 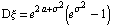 . .
Бета-распределение
Случайная величина x имеет
В-распределение (бета-распределение) с
параметрами a1 и a2, если ее
функция плотности вероятностей имеет вид:
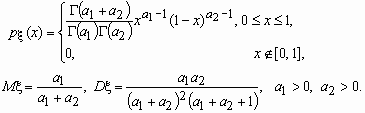
Распределение Вейбулла
Случайная величина x имеет
распределение Вейбулла с параметрами l
0 и a , если ее функция
распределения и функция плотности вероятностей
имеют соответственно вид:
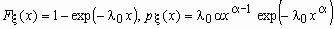 , , 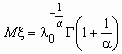 , , 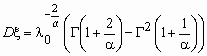 , , 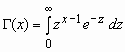 - гамма-функция Эйлера. - гамма-функция Эйлера.
Распределение Коши
Случайная величина x имеет
распределение Коши с параметрами a и c,
если ее функция распределения и функция
плотности вероятностей имеют соответственно
вид:
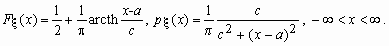
У распределения Коши не существует ни
математического ожидания, ни дисперсии. Это
распределение не имеет ни одного момента
положительного порядка.
Гамма-распределение
Случайная величина x имеет
Г-распределение (гамма-распределение) с
параметрами a и b, если ее функция
плотности вероятностей имеет вид:
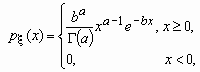 , a > 0, b
> 0, , a > 0, b
> 0, 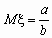 , , 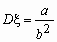 , , 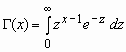 . .
Распределение Лапласа
Случайная величина x имеет
распределение Лапласа (двустороннее
экспоненциальное распределение) с параметром l , если ее функция плотности
вероятностей имеет вид:
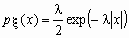 | , - | 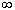 | < x < | 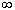 | , Mx = 0, Dx = 2/l 2. |

|

