Биномиальное
распределение ~ Геометрическое
распределение ~ Гипергеометрическое
распределение ~ Пуассоновское
распределение
Биномиальное распределение
Пусть проводится серия из n
независимых испытаний, каждое из которых
заканчивается либо “успехом” либо
“неуспехом”. Пусть в каждом испытании (опыте)
вероятность успеха p, а
вероятность неуспеха q = 1- p. С
таким испытанием можно связать случайную
величину x , значение которой
равно числу успехов в серии из n испытаний.
Эта величина принимает значения от 0
до n. Ее распределение называется биномиальным
и определяется формулой Бернулли
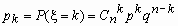 , 0 < p <1,
k = 0, 1, …, n, , 0 < p <1,
k = 0, 1, …, n, 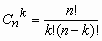 ,
Mx = np, Dx = npq, ,
Mx = np, Dx = npq, 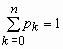 . .
Геометрическое распределение
Со схемой испытаний Бернулли можно
связать еще одну случайную величину x - число испытаний до первого успеха.
Эта величина принимает бесконечное множество
значений от 0 до +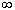 и ее распределение
определяется формулой и ее распределение
определяется формулой
pk = P(x= k) = qk-1 p, 0 <p <1, k=1,
2, … , 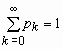 , ,
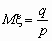 , , 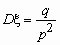 . .
Гипергеометрическое распределение
В партии из N изделий
имеется M (M < N) доброкачественных
и N - M дефектных изделий. Если
случайным образом из всей партии выбрать
контрольную партию из n изделий,
то число доброкачественных изделий в
контрольной партии - случайная величина, которую
обозначим x. Распределение
такой случайной величины называется гипергеометрическим
и имеет вид:
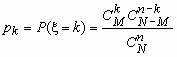 , k = 0, 1,
…, min(n,M), , k = 0, 1,
…, min(n,M), 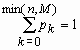 , ,
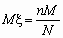 , , 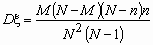 . .
Пуассоновское распределение
Пуассоновское распределение c параметром
l имеет случайная величина x , принимающая целые
неотрицательные значения k =
0, 1, 2, … с вероятностями pk:
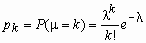 , , 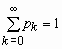 , Mx =l, Dx = l , l > 0 - параметр
распределения. , Mx =l, Dx = l , l > 0 - параметр
распределения.

|

