Определение
нуля ~ Нуль порядка n ~ Простой
нуль ~ Необходимое и достаточное
условия нуля порядка n ~ Порядок
нуля произведения анал. функций
Пусть функция f (z) является
аналитической в точке z0. Точка z0
называется нулем функции f (z), если ее
значение в этой точке равно нулю, т.е. f (z0)
= 0.
В разложении функции в ряд Тейлора в окрестности
нуля этой функции (т. z0) отсутствует
свободный член: С0 = f(z0) =
0.
Если при этом в разложении отсутствуют и
слагаемые, содержащие степени разности (z-z0)
до n-ой степени, т.е. разложение имеет вид:  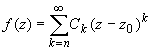 или или 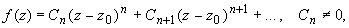 то
точка z0 называется нулем порядка n
функции f(z). то
точка z0 называется нулем порядка n
функции f(z).
Нуль первого порядка (n = 1) называется простым
нулем.
Следующие условия являются
необходимым и достаточным условиями нуля
порядка n функции f (z) в точке z0:
a). 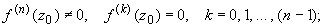
b). представление функции в виде произведения: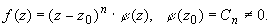
Порядок нуля в точке z0
функции, полученной в результате перемножения
аналитических функций
f (z) = f1(z) f2(z) равен сумме
порядков нуля (n1 + n2) в этой
точке функций сомножителей
( n1 - порядок нуля в точке z0
функции f1(z), n2 -
порядок нуля в точке z0 функции f2(z)
).
ПРИМЕР 1. Определить порядок нуля в точке для
функции f(z).
ПРИМЕР 2. Найти нули функции f(z) и
определить их порядок.
ПРИМЕР 3. Найти нули функции f(z) и
определить их порядок.
ПРИМЕР 4. Определить порядок нуля в точке для
функции f(z).

|

