Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример
4
Пример 1.
Определить порядок нуля z0 для функции
f (z) = ez -1-z.
Решение. Разложим функцию f
(z) по степеням z:
ez -1- z = (1 + z + z2/2! + z3/3!
+...) - 1 - z = z2/2! + z3/3! +...
Так как в полученном разложении коэффициент С2
= 1/2, т.е. не равен нулю, а предыдущие равны нулю С0
= С1 = 0, то заключаем, что точка z0
= 0 является нулем порядка n = 2 для заданной
функции.

Пример 2. Найти нули функции и определить их
порядок:
f (z) = (z4+2z+1)2(z2-2z+2).
Решение. Раскладываем f(z) (многочлен)
на множители:
f (z) = (z-i)4(z+i)2(z-(1+i))(z-(1+i)).
Находим нули функции: z1 = i, z2
= -i, z3 = 1+i, z4 = 1-i.
Определяем порядок каждого нуля.
Для точки z1 = i из равенства
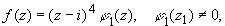
получаем, что z1 = i - нуль 4-го порядка.
Для точки z2 = -i аналогично
находим, что это нуль 4-го порядка:
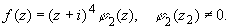
Из равенства
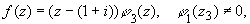
получаем, что z3 = 1+i - простой нуль.
Аналогично из
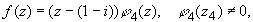
имеем z4 = 1-i тоже простой нуль
для f(z).
Уточним:
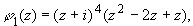
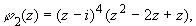
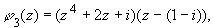
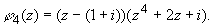

Пример 3.
Найти нули функции и определить их порядок:
f (z) = 1+ch z.
Решение. Решая уравнение 1+ch z = 0,
имеем:
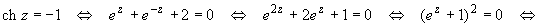

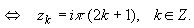
Находим производные заданной функции и их
значения в точках zk: 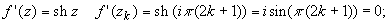 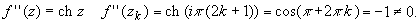
Так как
f (zk) = f '(zk) = 0 и 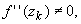 то то 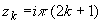
является нулями второго порядка функции
f (z) = 1 + ch z.

Пример 4. Определить порядок нуля z0 = 0
функции:
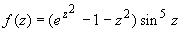 . .
Решение. Функция f (z)
задана в виде произведения двух функций:
f (z) = f1(z)f2(z), где
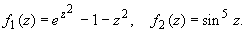
Вычисляем порядок нуля в точке z0 = 0 для
третьего сомножителя f1(z).
Записываем f1(z) в виде:
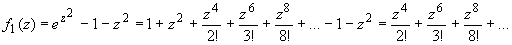
Следовательно, z0 = 0 является
нулем 4-го порядка (n1 = 4) для функции f1(z).
Для функции f2(z) = sin z
точка z0 = 0 - нуль первого порядка, т.к.
sin'(0) = cos(0) = 1 (т.е. не равно нулю). Поэтому, учитывая,
что f2(z) = sin5 z = sin z
sinz sin z sin z sin z,
получаем, что z0 = 0 - нуль 5-го порядка (n2
= 5) порядка для f2(z).
Поскольку f (z) = f1(z)
f2(z), то получаем, что точка z0
= 0 является нулем 9-го порядка заданной функции, т.к.
n = n1 + n2 = 4+5 = 9.

|

