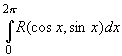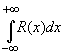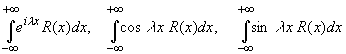
~           ~       

Утверждение. Пусть R(x, y) - рациональная функция двух действительных переменных. Тогда справедливы равенства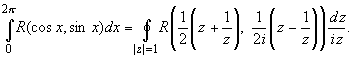

Действительно, замена z = e^ix переводит отрезок 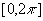     в окружность |z| = 1,
.
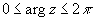При этом: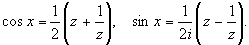  

В результате имеем формулу, сопоставляющую интеграл от действительной переменной с интегралом по замкнутой кривой от функции комплексного переменного:  

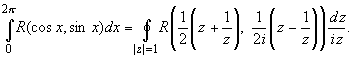
ПРИМЕР 1. Вычисление интеграла.

Замечание. Для вычисления таких интегралов в математическом анализе в общем случае, за исключением некоторых частных случаев, применяется замена tg(1/2)= t ("универсальная" подстановка) и интеграл приводится к интегралу от рациональной дроби.

Утверждение. Пусть функция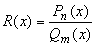  
где P_n(x) и Q_m(x) - многочлены степени n и m (n = const, m = const), удовлетворяет условиям:
1. (m - n) больше или равно 2.
2. Q_m(x) не равна 0 при x, принадлежащим области действительных чисел.
Тогда справедливы равенства:


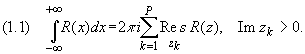
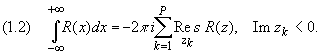
Здесь z_k, k = 1,2,..., p - все особые точки функции R(z), расположенные выше оси Ох (Im z_k> 0) в случае формулы (1) и ниже оси Ох (Im z_k< 0) в случае формулы (1.2).

Замечание. Если R(z) - четная функция, то можно, используя формулы (1.1) и (1.2), вычислить интеграл вида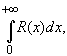  
т.к. для четной функции имеет место равенство:   

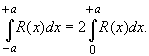
ПРИМЕР 2. Вычисление интеграла.

Утверждение. Пусть R(x) - рациональная функция, не имеющая особых точек на действительной оси, для которой точка z, равная бесконечности, - нуль порядка не ниже первого (т.е. (m - n) больше или равно 1). Тогда справедливы формулы:

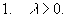
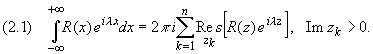
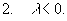
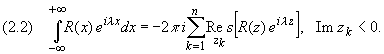
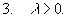
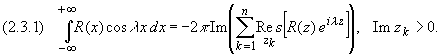
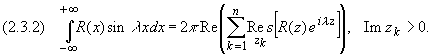
ПРИМЕР 3. Вычисление интеграла.