Пример 1 ~ Пример 2.1 ~ Пример 2.2 ~ Пример
3.1 ~ Пример 3.2 ~ Пример 3.3
Пример 1.
Вычислить интеграл: 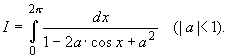
Положим z = e ix, тогда cos x = (z +
z - 1)/2. Вычислим dz = d(e ix),
откуда dx = (dz)/(iz), а исходный интеграл
запишется в виде:
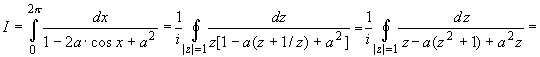
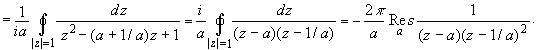
Так как при |a|<1, подинтегральная
функция 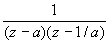 внутри круга внутри круга 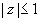
имеет один полюс первого порядка в точке z = a.
Поскольку 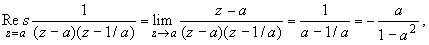
будем иметь
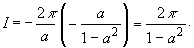

Пример 2.1. Вычислить интеграл: 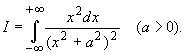
Рассмотрим функцию 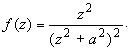
Она является аналитической функцией, имеющей
полюсы второго порядка в точках 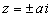 и в бесконечности имеет нуль
второго порядка. и в бесконечности имеет нуль
второго порядка.
Согласно формуле (1.1) имеем
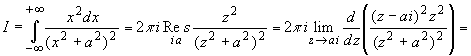
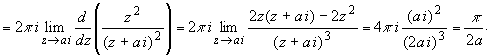

Пример 2.2.
Вычислить интеграл: 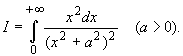
Используя результаты вычисления
интеграла в примере 2.1 (обозначив его как I1),
вычислим данный интеграл: 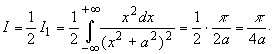

Пример 3.1. Вычислить интеграл: 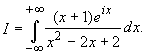
Функция 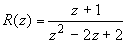 в точке z, равной
бесконечности, имеет нуль первого порядка и на
действительной оси не имеет особых точек. в точке z, равной
бесконечности, имеет нуль первого порядка и на
действительной оси не имеет особых точек.
Особые точки функции z1 = 1 + i,
z2 = 1 - i.
Поскольку 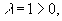 вычисляем вычет
в точке z1 = (1 + i) - простом полюсе
функции R(z) eiz: вычисляем вычет
в точке z1 = (1 + i) - простом полюсе
функции R(z) eiz:
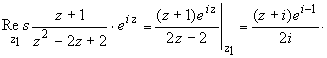
Для заданного интеграла по формуле (2.1) получаем
результат
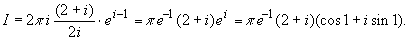

Пример 3.2. Вычислить интеграл: 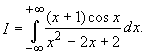
Так как 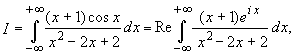 поэтому,
используя результат примера 3.1, получаем: поэтому,
используя результат примера 3.1, получаем:
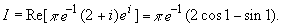

Пример 3.3. Вычислить интеграл: 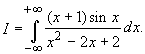
Так как 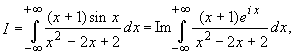 то используя
результат примера 3.1, получаем: то используя
результат примера 3.1, получаем:
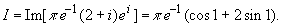

|

