Уравнение с разделяющимися переменными ~ Общий интеграл ~  Решение задачи Коши

Уравнением с разделяющимися переменными называется уравнение первого порядка вида

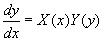
где X(x) и Y(y) — непрерывные функции.

Общий интеграл уравнения задается выражением

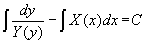
Решение y = y(x) задачи Коши y(x₀) = y₀  как неявную функцию переменной x задает выражение

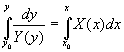
ПРИМЕР 1.   Уравнение с разделяющимися переменными. Общее решение.

ПРИМЕР 2. Уравнение с разделяющимися переменными. Решение  задачи Коши.

Заметим, что если Y(y*) = 0 в некоторой точке y*, то уравнение
y' = Y(y)X(x) имеет решение y(x) = y* при всех допустимых x.
Все решения системы исчерпываются выражениями  y(x) = y* и

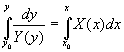
ПРИМЕР 3. Уравнение с разделяющимися переменными, имеющее два семейства решений.

ПРИМЕР 4. Уравнение с разделяющимися переменными, имеющее несколько семейств решений.