Пределы
суммы, произведения и частного
последовательностей ~ Неопределенности
и их раскрытие
Пределы суммы, произведения и частного
последовательностей.
Пусть заданы две последовательности 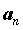 и и 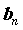 . Если
существуют . Если
существуют 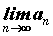 и и 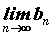 , то существуют и пределы суммы и произведения
последовательностей, а при , то существуют и пределы суммы и произведения
последовательностей, а при 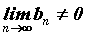 и предел частного,
причем и предел частного,
причем 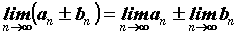 , , 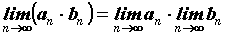 , , 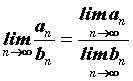 . Для правильного
применения этих теорем очень важно
существование пределов каждой
последовательности. . Для правильного
применения этих теорем очень важно
существование пределов каждой
последовательности.
ПРИМЕР 1 . Простейшие методы
вычисления пределов последовательностей
Неопределенности и их раскрытие.
Если 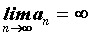 и и 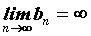 , то может существовать , то может существовать 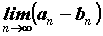 . В этом
случае говорят, что имеем неопределенность
типа . В этом
случае говорят, что имеем неопределенность
типа 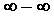 . Также может существовать . Также может существовать 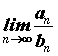 , в этом
случае имеем неопределенность типа , в этом
случае имеем неопределенность типа 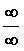 .
Если .
Если 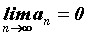 и и 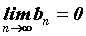 , то может существовать , то может существовать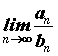 . В этом случае
говорят, что имеем неопределенность типа . В этом случае
говорят, что имеем неопределенность типа 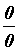 .
Поскольку в перечисленных случаях не применимы
теоремы о пределе суммы, произведения и частного,
используют другие способы вычисления, которые
называют методами раскрытия неопределенностей.
Это, как правило, алгебраические преобразования,
приводящие выражения к виду, при котором можно
пользоваться упомянутыми теоремами. .
Поскольку в перечисленных случаях не применимы
теоремы о пределе суммы, произведения и частного,
используют другие способы вычисления, которые
называют методами раскрытия неопределенностей.
Это, как правило, алгебраические преобразования,
приводящие выражения к виду, при котором можно
пользоваться упомянутыми теоремами.
ПРИМЕР 2 . Методы раскрытия
неопределенностей

|

