Интегрирование
рациональных функций ~ Интегрирование
тригонометрических функций ~ Интегрирование
иррациональных функций
Интегрирование рациональных функций -
Функция 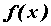 называется рациональной,
если она вычисляется с помощью четырех
арифметических действий, то есть в общем случае
является частным от деления двух многочленов: называется рациональной,
если она вычисляется с помощью четырех
арифметических действий, то есть в общем случае
является частным от деления двух многочленов: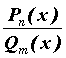 . Если . Если 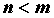 , рациональная дробь
называется правильной. Неопределенный
интеграл от рациональной функции всегда можно
вычислить. Для этого: , рациональная дробь
называется правильной. Неопределенный
интеграл от рациональной функции всегда можно
вычислить. Для этого:
Если 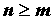 , выделяем целую часть
рациональной дроби с помощью деления многочлена
на многочлен. Правильную рациональную дробь (или
правильный остаток от деления) раскладываем на
простейшие дроби. Вид разложения определяется
корнями многочлена , выделяем целую часть
рациональной дроби с помощью деления многочлена
на многочлен. Правильную рациональную дробь (или
правильный остаток от деления) раскладываем на
простейшие дроби. Вид разложения определяется
корнями многочлена 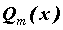 , а
именно: , а
именно:
Каждому действительному корню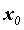 кратности 1 в разложении соответствует член
кратности 1 в разложении соответствует член 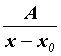 . .
Каждому действительному корню 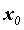 кратности
кратности 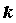 в разложении
соответствует набор из в разложении
соответствует набор из 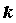 членов членов
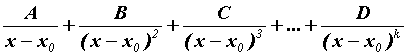 . .
Каждой паре комплексно сопряженных корней 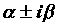 кратности 1 в разложении соответствует
член кратности 1 в разложении соответствует
член 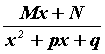 ( (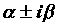 - корни
уравнения - корни
уравнения 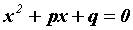 ). ).
Каждой паре комплексно сопряженных корней
кратности 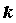 в разложении
соответствует набор из в разложении
соответствует набор из 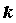 членов членов
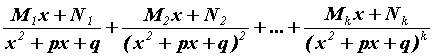 . .
В приведенных выражениях 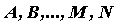 -
неопределенные коэффициенты, которые можно
найти, приводя разложение обратно к общему
знаменателю -
неопределенные коэффициенты, которые можно
найти, приводя разложение обратно к общему
знаменателю 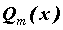 , приравнивая полученные
коэффициенты при степенях , приравнивая полученные
коэффициенты при степенях 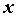 к
соответствующим коэффициентам к
соответствующим коэффициентам 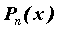 и решая
систему относительно и решая
систему относительно 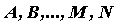 . .
Наконец, полученное разложение интегрируем
почленно.
ПРИМЕР 1 . Интегрирование
рациональных функций
Интегрирование тригонометрических
функций - Интегралы вида 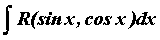 , где , где 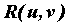 - рациональная функция своих аргументов,
вычисляются с помощью универсальной замены
переменной - рациональная функция своих аргументов,
вычисляются с помощью универсальной замены
переменной 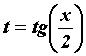 . При
этом . При
этом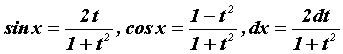 . Однако универсальная замена
обычно связана с большими вычислениями, поэтому
в некоторых случаях можно ее избежать. . Однако универсальная замена
обычно связана с большими вычислениями, поэтому
в некоторых случаях можно ее избежать.
Интегралы вида 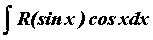 вычисляются с помощью замены
вычисляются с помощью замены 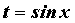 . Интегралы вида . Интегралы вида 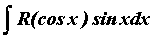 вычисляются
с помощью замены вычисляются
с помощью замены 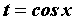 .
Интегралы вида .
Интегралы вида 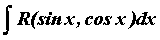 , если , если 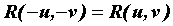 , то есть четная рациональная функция
своих аргументов вычисляются с помощью замены , то есть четная рациональная функция
своих аргументов вычисляются с помощью замены
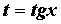 . .
Интегралы вида 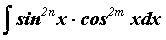 вычисляются
с помощью формул понижения степени вычисляются
с помощью формул понижения степени 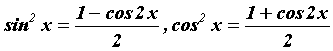 . .
ПРИМЕР 2 . Интегрирование
тригонометрических функций
Интегрирование иррациональных функций -
Общий принцип интегрирования иррациональных
выражений заключается в замене переменной,
позволяющей избавиться от корней в
подынтегральном выражении. Для некоторых
классов функций эта цель достигается с помощью
стандартных замен.
Интегралы вида 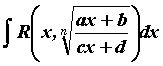 , где , где 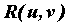 - рациональная функция своих аргументов,
вычисляются заменой - рациональная функция своих аргументов,
вычисляются заменой 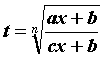 . .
Интегралы вида 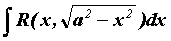 вычисляются заменой
вычисляются заменой 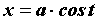 или или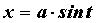 . .
Интегралы вида 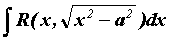 вычисляются заменой
вычисляются заменой 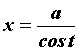 или или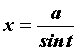 . Интегралы вида . Интегралы вида 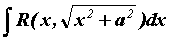 вычисляются
заменой вычисляются
заменой 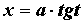 или или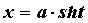 . .
ПРИМЕР 3 . Интегрирование
иррациональных функций

|

