СЛАУ ~ Матричная форма записи ~ Решение матричных уравнений ~ Формулы Крамера ~ Метод Гаусса

Рассмотрим систему линейных алгебраических уравнений (СЛАУ) относительно n неизвестных x₁ , x₂ , ..., x_n:

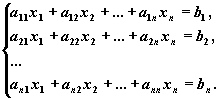
Эта система в "свернутом" виде может быть записана так:

S ⁿ_i=1a_ij x_j = b_i , i=1,2, ..., n.

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме Ax=b, где

, , .

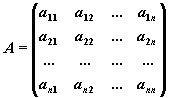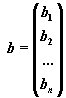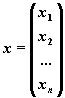Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец x, элементы которой - искомые неизвестные, называется решением системы.

Система линейных алгебраических уравнений, записанная в виде Ax=b, является матричным уравнением.

Если матрица системы невырождена, то у нее существует обратная матрица и тогда решение системы Ax=b дается формулой:

x=A ^-1 b.

ПРИМЕР 1. Решение матричного уравнения.

Справедливо следующее утверждение (формулы Крамера).

Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x₁ , x₂ , ..., x_n, определяемое формулами Крамера

x_i =D_i / D, i=1,2, ..., n,

где D_i - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.

ПРИМЕР 2. Вычисление решения системы линейных уравнений по формулам Крамера.

Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x₁ , x₂ , ..., x_n

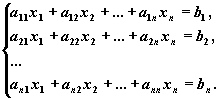
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

решение которой находят по рекуррентным формулам:

x_n =d_n , x_i = d_i -S ⁿ_k=i+1 c_ik x_k , i=n-1, n-2, ...,1.

Матричная запись метода Гаусса.

1. Прямой ход метода Гаусса: приведение расширенной матрицы системы

     
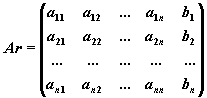
   к ступенчатому виду

            
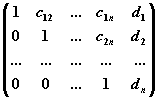
   с помощью элементарных операций над строками матрицы (под элементарными операциями понимаются следующие операции:

   • перестановка строк;
   • умножение строки на число, отличное от нуля;
   • сложение строки матрицы с другой строкой, умноженной на отличное от нуля чиcло).
2. Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица
   ,
   последний, (n+1)-й, столбец этой матрицы содержит решение системы.

ПРИМЕР 3. Решение системы линейных уравнений методом Гаусса.