Определения. Разложение определителя по 1-ой строке ~ Разложение определителя по i-ой строке и j-ому столбцу ~ Определители матриц 2 и 3 порядков

Пусть A квадратная матрица порядка n, n>1. Определителем квадратной матрицы A порядка n называется число

det A= = ,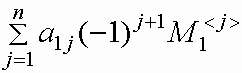

где M₁ ^<j> - определитель квадратной матрицы порядка n -1, полученной из матрицы A вычеркиванием первой строки и j -го столбца, называемый минором элемента a_1j .

Формула
det A =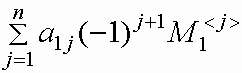 
называется формулой вычисления определителя разложением по первой строке.
Число (-1) ^j+1 M₁ ^<j> называется алгебраическим дополнением элемента a_1j.

Пусть M_i ^<j> - определитель квадратной матрицы порядка n-1, полученной из матрицы A вычеркиванием i-й строки и j-го столбца (минор элемента a_ij ).
Число (-1) ^j+i M_i ^<j> называется алгебраическим дополнением элемента a_ij матрицы A.
Справедливы формулы вычисления определителя квадратной матрицы A разложением по i-й строке и разложением по j-му столбцу:

det A= = =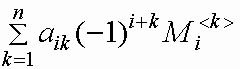
=

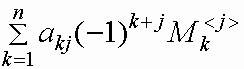
для i=1,2,...,n, j=1,2,...,n.

ПРИМЕР 1. Вычисление определителя разложением по 1-ой строке.

Для квадратной матрицы второго порядка формула вычисления определителя упрощается:

det 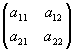= = 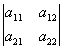a₁₁ a₂₂ - a₁₂ a₂₁,

поскольку, например, в формуле разложения определителя по 1-ой строке 
M₁ ^{< 1>} =a₂₂ , M₁ ^{< 2>} =a₂₁.

Для квадратной матрицы третьего порядка формула вычисления определителя разложением по 1-ой строке имеет вид:

=-+.

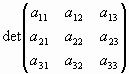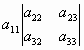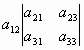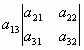ПРИМЕР 2. Вычисление определителей матриц 2 и 3 порядков.