  Все итеративные процессы в Mathcad
основаны на дискретных аргументах. Если не
обращать внимание на способ определения, то
дискретный аргумент выглядит как обычная
переменная. Различие в том, что обычная
переменная принимает только одно значение, в то
время как дискретный аргумент принимает ряд
значений, отделяемых одинаковыми шагами.
Например, можно определить дискретный аргумент,
чтобы пройти от -4 до 4 с шагом 2. Если теперь
использовать этот дискретный аргумент в
выражении, Mathcad вычислит это выражение пять раз,
один раз для каждого значения, принимаемого
дискретным аргументом. Все итеративные процессы в Mathcad
основаны на дискретных аргументах. Если не
обращать внимание на способ определения, то
дискретный аргумент выглядит как обычная
переменная. Различие в том, что обычная
переменная принимает только одно значение, в то
время как дискретный аргумент принимает ряд
значений, отделяемых одинаковыми шагами.
Например, можно определить дискретный аргумент,
чтобы пройти от -4 до 4 с шагом 2. Если теперь
использовать этот дискретный аргумент в
выражении, Mathcad вычислит это выражение пять раз,
один раз для каждого значения, принимаемого
дискретным аргументом.
Без дискретных аргументов было бы невозможным
полное использование возможностей Mathcad. Этот
раздел показывает, как определять и использовать
дискретные аргументы, чтобы выполнять
многократные вычисления.
Определение и использование дискретного
аргумента
Чтобы определять дискретный аргумент,
напечатайте имя переменной, сопровождаемое
двоеточием и диапазоном значений. Например, вот
как определить переменную j, принимающую
значения от 0 до 15:
- Напечатайте j и затем нажмите клавишу двоеточия
(:). Пустое поле указывает, что Mathcad ожидает
определение для j. В этот момент Mathcad не знает,
будет ли j обычной переменной или дискретным
аргументом.
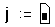
- Напечатайте 0.Затем нажмите клавишу точки с
запятой (;). Это сообщает Mathcad, что
определяется дискретный аргумент. Mathcad
показывает точку с запятой как две точки .., что
означает диапазон. Завершите определение
дискретного аргумента, печатая 15 в оставшемся
поле.
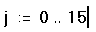
Это определение указывает, что j принимает
значения 0,1,2...15. Чтобы определять дискретный
аргумент, который изменяется с шагом, отличным от
1, см. подраздел “Типы
диапазонов” ниже в этой главе.
Если только дискретный аргумент определён, он
принимает полный диапазон значений каждый раз,
когда он используется. Если дискретный
аргумент используется, например, в выражении,
Mathcad должен вычислить это выражение для каждого
значения дискретного аргумента.
Следует определять дискретный аргумент в
точности, как показано выше. Должны быть:
- имя переменной слева,
- или := или
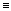 в середине, и в середине, и
- допустимый диапазон справа.
Обратите внимание, что нельзя определять
простую переменную через дискретный аргумент.
Например, если, определив j, как показано,
теперь записать , то Mathcad истолкует это как
попытку приравнять скалярную переменную
дискретному аргументу, и отметит уравнение
сообщением “нескалярная величина”.
Дискретный аргумент может применяться для
присвоения значений элементам вектора или
матрицы. Можно определять элементы вектора,
используя дискретный аргумент как нижний индекс.
Например, чтобы определить для каждого значения
j:
- наберите x[j:j^2[Space]+1
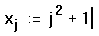
Рисунок 1 показывает вектор значений,
вычисленных по этой формуле. Поскольку j —
дискретный аргумент, вычисления по формуле
делаются для каждого значения j. Это
определяет для каждого значения j от 0 до 15.
Результат точно такой же, как если бы напечатать
| x0 := 02 + 1 |
| x1 := 12 + 1 |
| . |
| . |
| . |
| x15 :=152 + 1 |
Чтобы понимать, как Mathcad вычисляет при
помощи переменных диапазона, имейте в виду
основной принцип:
Если дискретный аргумент используется в
выражении, Mathcad вычисляет выражение один раз для
каждого значения дискретного аргумента.
Этот принцип выражает различие между
выражениями с дискретным аргументом и без него.
Выражения, которые не содержат дискретный
аргумент, имеют только одно значение. Выражения,
содержащие дискретные аргументы, принимают
много значений, которые соответствуют каждому
значению каждого дискретного аргумента.
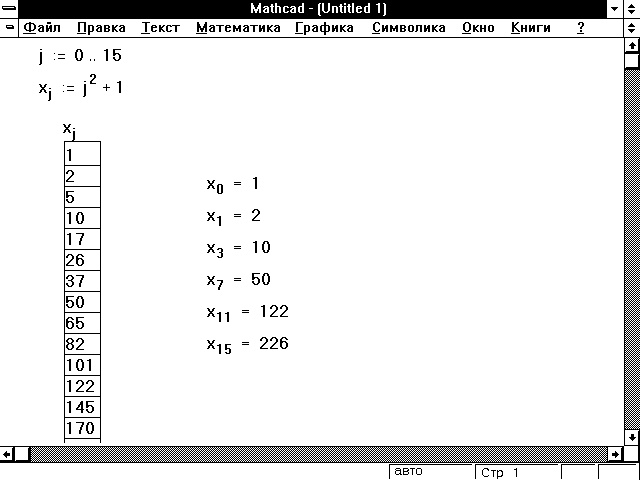
Рисунок 1: Использование дискретного аргумента
для определения элементов вектора x.
Если в формуле используются два или более
дискретных аргумента, Mathcad вычисляет формулу
один раз для каждого значения каждого
дискретного аргумента. Это обсуждается
подробнее в разделе “Итерационные
вычисления” ниже в этой главе.
Mathcad требует больше времени для вычисления
формул, содержащих дискретный аргумент,
поскольку приходится выполнять многократные
вычисления. Форма курсора изменяется во время
вычислений. Чтобы прервать вычисления, нажмите
[Esc]. Чтобы возобновить вычисления, щёлкните мышью
на формуле и нажмите [F9].
Типы диапазонов
Определение j в предыдущем разделе является
самым простым типом определения диапазона. Mathcad
допускает дискретные аргументы со значениями,
расположенными от любого значения до любого
другого значения и меняющимися с произвольным
шагом.
Вот как выглядит определение произвольного
дискретного аргумента. Напечатайте:
k:1,1.1;2
Это будет выглядеть как:
k := 1,1.1..2
В этом определении диапазона:
- Переменная k — имя дискретного
аргумента. Это должно быть простое имя. Никакие
нижние индексы или функциональные определения
не допустимы.
- Число 1 — первое значение, принимаемое
аргументом k.
- Число 1.1 — второе значение в диапазоне. Обратите
внимание, что это не размер шага. Размер шага
в этом примере 0.1, разница между 1.1 и 1. Если
опустить запятую и 1.1, Mathcad примет размер шага
равным 1 в подходящем направлении.
- Число 2 — последнее значение в диапазоне. В этом
примере значения аргумента постоянно
увеличиваются. Если бы записать , то k проходил бы
значения от 10 до 1. Если третье число в
определении диапазона не равно целому числу
приращений начального значения, аргумент всё
равно не выйдет за его пределы. Например, пусть
определили k := 10, 20 ..60, тогда k будет принимать
значения 10, 20, 30... 60.
Можно использовать произвольные скалярные
выражения вместо 1, 1.1 и 2. Однако эти значения
должны всегда быть вещественными числами.
Комплексные числа не имеют смысла в определениях
дискретного аргумента, потому что имеется
бесконечное число путей, соединяющих два данных
комплексных числа. Рисунок 2 показывает
результаты различных определений дискретного
аргумента.
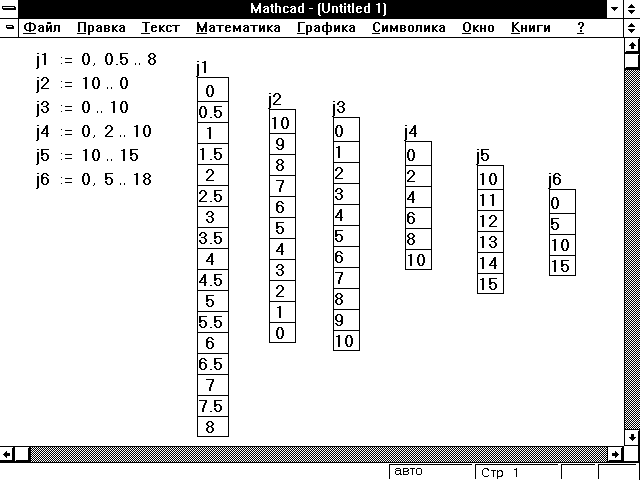
Рисунок 2: Некоторые допустимые определения
дискретного аргумента.
Обратите внимание, что, если для дискретного
аргумента используется дробное приращение,
нельзя использовать этот дискретный аргумент
как нижний индекс, поскольку нижние индексы
должны быть целыми числами.
  
|

