|
2. СИНТЕЗ СЛЕДЯЩЕЙ СИСТЕМЫ УПРАВЛЕНИЯ
2.1 Построение дискретной стохастической модели объекта
Полученная в пункте 1.3.1 динамическая линейная модель не учитывает множества факторов производства, хранения и сбыта товара. Возместим это, введя белый гауссовский шум. В результате получим уравнение, описывающее линейный объект в виде:
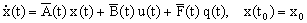 |
(2.1.1) |
где внешние возмущения q(t) являются последовательностями белых гауссовских шумов с характеристиками:
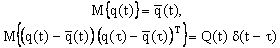 |
(2.1.2) |
и матрицей влияний 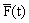 , значения которой получены экспериментально. , значения которой получены экспериментально.
Заметим, что модель (1.3.3) сформулирована в терминах дифференциальных уравнений лишь исходя из удобства теоретического анализа и простоты записи. Для экономической системы более адекватным является описание в терминах уравнений дискретного времени, когда время меняется с интервалом равным расчётному периоду (день, неделя, декада, месяц, зависимости от типа товара). Такая модель может быть получена из (1.3.3) формальным процессом дискретизации, т.е. заменой производных dZ/dt и dV/dt на отношение конечных разностей  Z/ Z/ t и t и  V/ V/ t, но может быть сформулирована и непосредственно в дискретном времени. t, но может быть сформулирована и непосредственно в дискретном времени.
Построение дискретной модели, эквивалентной непрерывной вида (2.1.1) будем осуществлять в предположении, что шаг дискретизации 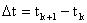 является постоянным и совпадает с периодом квантования управляющего сигнала, а момент дискретизации является постоянным и совпадает с периодом квантования управляющего сигнала, а момент дискретизации 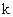 - с моментом приложения управляющих воздействий ( - с моментом приложения управляющих воздействий (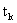 - момент квантования). - момент квантования).
Причём управление является кусочно-постоянным на каждом интервале управляющих воздействий, т.е.  . .
Тогда можно ограничится описанием поведения объекта в моменты квантования и, использовав для этого разностные уравнения, записать дискретный аналог для системы:
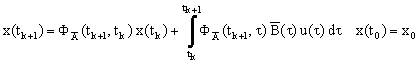 |
(2.1.3) |
где 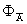 - фундаментальная матрица решений соответствующей однородной системы. - фундаментальная матрица решений соответствующей однородной системы.
Фундаментальную матрицу, по её свойству, можно представить в виде:
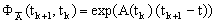 |
(2.1.4) |
а матричную экспоненту, в свою очередь - в виде ряда:
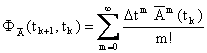 |
(2.1.5) |
Вычислив интеграл по формуле правых прямоугольников, запишем дискретную систему в разностной форме:
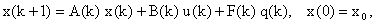 |
(2.1.6) |
где 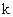 соответствует моменту времени соответствует моменту времени 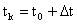 , матрицы A(k) и B(k) имеют вид: , матрицы A(k) и B(k) имеют вид:
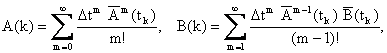 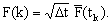 |
(2.1.7) |
Использование представления матричной экспоненты в виде ряда (2.1.5) позволяет достаточно легко регулировать точность квантования непрерывной информации на ЭВМ, которую можно определять точностью вычисления фундаментальной матрицы системы:
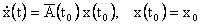 |
(2.1.8) |
дискретный аналог которой имеет вид:
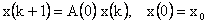 |
(2.1.9) |
где 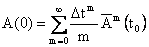 . .
Если обозначить через 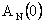 сумму сумму 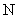 первых членов ряда (1.2.5), то матрица первых членов ряда (1.2.5), то матрица 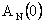 аппроксимирует аппроксимирует 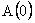 с погрешностью порядка с погрешностью порядка 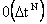 . При этом число слагаемых в . При этом число слагаемых в 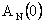 можно задавать заранее (вычисление с фиксированной точностью) или определять автоматически с помощью соотношения: можно задавать заранее (вычисление с фиксированной точностью) или определять автоматически с помощью соотношения:
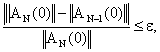 |
(2.1.10) |
где 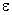 выбирается из условия обеспечения максимальной точности вычислений на ЭВМ конкретного типа. выбирается из условия обеспечения максимальной точности вычислений на ЭВМ конкретного типа.
В частном случае при N = 1 получаем решение системы дифференциальных уравнений (2.1.1) методом Эйлера, а при N = 4 - методом Рунге-Кутта.
Для соответствия модели (2.1.1) модели (1.3.2.1) к последней добавлено слагаемое F(k) q(k), где F(k) рассчитывается по (2.1.7); внешние возмущения q(k) являются последовательностями дискретных белых гауссовских шумов с характеристиками:
 |
(2.1.11) |
Полученная дискретная модель будет использоваться при численном моделировании.
2.2 Описание канала измерений
Измерение состояния модели объекта осуществляется в дискретные моменты времени 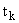 измерительным комплексом типа: измерительным комплексом типа:
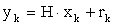 |
(2.2.2) |
где 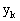 - n - мерный вектор измерений, - n - мерный вектор измерений, 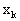 - n - мерный вектор состояния, H - матрица - n - мерный вектор состояния, H - матрица
канала измерений, заданная следующим образом:
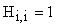 , если i-тая компонента вектора состояния измеряема; , если i-тая компонента вектора состояния измеряема;
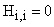 , в противном случае; , в противном случае;
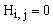 , если , если 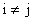 , где , где 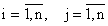 ; ;
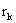 - последовательность гауссовских шумов с характеристиками: - последовательность гауссовских шумов с характеристиками:
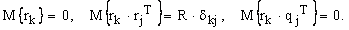 |
(2.2.2) |
2.3 Оценивание состояния фильтром Калмана
Для учёта погрешности измерения, погрешности моделирования вектора состояния и влияния на систему случайных факторов воспользуемся дискретным фильтром Калмана для оценки вектора состояния.
Текущие значения оценок вектора состояния 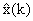 определяются по итерационному правилу: определяются по итерационному правилу:
  |
(2.3.2) |
где y(.) - канал измерений (2.2.1), H - матрица канал измерений, I - единичная матрица соответствующей размерности, 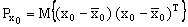 - матрица ковариаций начального вектора состояния. - матрица ковариаций начального вектора состояния.
Модель является стохастической, и не все компоненты вектора состояний могут быть измерены. Например: V-количество товара у потребителей, скорее всего, нужно считать неизмеряемой величиной. Остальные компоненты вектора состояний измеряются с некоторой погрешностью, поэтому оценим значения вектора состояний фильтром Калмана. Для этого введём стохастический канал измерений, вида:
 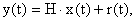 где где 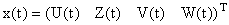 , ,
r(t) - погрешность измерений, которую будем описывать белыми гауссовскими шумами. H- матрица вида:
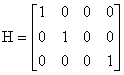 , если Z (количество товара на рынке) - неизмеряемая величина; , если Z (количество товара на рынке) - неизмеряемая величина;
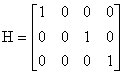 , если V (количество товара у потребителей) - неизмеряемая величина; , если V (количество товара у потребителей) - неизмеряемая величина;
 , если Z и V - неимеряемые величины. , если Z и V - неимеряемые величины.
В результате оценки вектора состояний фильтром Калмана получим, что оценка практически полностью совпадает со значениями вектора состояний полученными в результате моделирования.
|

