|
1.ПОСТРОЕНИЕ МОДЕЛИ ПРОИЗВОДСТВА, ХРАНЕНИЯ И СБЫТА ТОВАРА ПОВСЕДНЕВНОГО СПРОСА
Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств.
Моделирование позволяет с меньшими затратами воссоздать процесс и выявить критерии его оптимизации. К сожалению, очень трудно воссоздать модель, отвечающую всем характеристикам объекта. Не всегда возможно создание материальных моделей, воспроизводящих физические и функциональные характеристики изучаемого объекта, поэтому гораздо эффективней использовать абстрактное моделирование. В настоящее время широко применяется два вида математического моделирования: аналитическое и имитационное. Аналитическое моделирование позволяет получать более точное решение, формируя математические законы, связывающие объекты системы, записанные в виде некоторых функциональных соотношений. Задачей аналитического моделирования является решение уравнений для получения теоретических результатов и сопоставление этих результатов с практикой. К достоинствам аналитического моделирования можно отнести большую силу обобщения, многократность использования, но наиболее полное исследование процесса функционирования системы можно провести, если известны явные зависимости связывающие искомые характеристики с начальными условиями, параметрами и переменными системы. Однако такие зависимости удается получить для сравнительно простых систем. Чтобы использовать аналитический метод необходимо существенно упростить первоначальную модель, чтобы иметь возможность изучить общие свойства системы. Более сложные задачи можно решать методом имитационного моделирования при условии, что не существует законченной математической постановки данной задачи, либо еще не разработаны аналитические методы решения сформулированной математической модели, либо если аналитические модели имеются, но процедуры столь сложны и трудоемки, что имитационное моделирование дает более простой способ решения задачи. Имитационные модели позволяют достаточно просто учитывать случайные воздействия и другие факторы, которые создают трудности при аналитическом исследовании. Данная модель позволяет проводить эксперименты, меняя при этом условия протекания процесса, и, в конечном счете, определить такие условия, при которых результат удовлетворяет требованиям. Данный метод позволяет понять поведение процесса или объекта и выбрать стратегию, обеспечивающую наиболее эффективное ее функционирование. Имитационное моделирование, как правило, осуществляется при помощи компьютеров и воспроизводит процесс функционирование системы во времени, имитируя явления, составляющие процесс с сохранением их логической структуры. Данные модели осуществляют прогон программы с заданными параметрами. Под имитацией понимают проведение на компьютерах различных серий экспериментов с моделями, которые представлены в качестве некоторого набора (комплекса) компьютерных программ. Сравнение характеристик (конструкций, управлений) моделируемого объекта осуществляется путем вариантных просчетов.
Имитационное моделирование имеет ряд недостатков. Исследования с помощью этого метода обходятся дорого - необходимо большое количество машинного времени, поскольку метод основывается на статистических испытаниях и требует многочисленных прогонов программ; модель разрабатывается для конкретных условий и, как правило, не тиражируется. Велика вероятность ложной имитации, что делает необходимым тщательный анализ результатов имитационного моделирования. Успех или неудача в применении имитационных моделей в большей степени зависит не от метода, а от того, как он применяется.
Исходя из вышеизложенных рассуждений, можно сделать вывод, что для воссоздания (имитации) реального экономического процесса (деятельности предприятия) целесообразней будет воспользоваться именно имитационным моделированием, как методом компьютерного моделирования.
1.1 Основные определения и обозначения
Для построения имитационной математической модели производства хранения и сбыта продукции используется идея, предложенная в [3].
При построении модели используются следующие обозначения переменных и параметров модели:
Х - общее количество единиц товара, выпущенных предприятием;
U - темп производства товара (количество единиц товара, выпущенных в единицу времени);
Z - количество товара на рынке;
V - количество товара у потребителей (ещё не потреблённого);
 W- доход (разница между выручкой и затратами на единицу времени); W- доход (разница между выручкой и затратами на единицу времени);
Y- потенциальный спрос (полное количество товара, способного мгновенно удовлетворить спрос в условиях отсутствия ажиотажного спроса);
C - цена товара (C>1, так как себестоимость товара считается равной 1);
K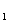 - темп потребления товара (относительный коэффициент потребления купленного товара в единицу времени); - темп потребления товара (относительный коэффициент потребления купленного товара в единицу времени);
K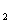 - плата за хранение единицы непроданного товара в единицу времени; - плата за хранение единицы непроданного товара в единицу времени;
N(C) - коэффициент скорости продажи товара.
Параметры Y, K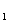 , K , K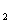 считаются постоянными. Величины U,C (темп производства и продажная цена) назначаются производителем и могут быть как постоянными, так и переменными. Переменные X, Z, V, W - функции времени и могут изменяться в соответствии с законами рынка. считаются постоянными. Величины U,C (темп производства и продажная цена) назначаются производителем и могут быть как постоянными, так и переменными. Переменные X, Z, V, W - функции времени и могут изменяться в соответствии с законами рынка.
1.2 Построение статической модели
Статическая модель описывает один цикл производства и сбыта: выработанный за расчётную единицу времени товар поступает на рынок и продаётся, в результате получается определённый доход; все эти действия происходят в одну расчётную единицу времени. Ясно, что в равновесном состоянии система характеризуется двумя соотношениями баланса:
- Поступившее на рынок количество товара равно проданному;
- Сколько товара продано населению столько и потреблено.
Распишем эти соотношения на языке введенных обозначений. За единицу времени прирост товара на рынке составляет U единиц. Количество товара на рынке составляет Z единиц, количество товара у потребителя - V единиц. В состоянии равновесия оба количества постоянны. Будем считать, что в единицу времени продаётся 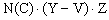 единиц товара, где Y-V текущий спрос, N(C) -коэффициент, зависящий от цены С (скорость продажи пропорциональна спросу и количеству товара на рынке). Тогда указанные соотношения баланса имеют вид: единиц товара, где Y-V текущий спрос, N(C) -коэффициент, зависящий от цены С (скорость продажи пропорциональна спросу и количеству товара на рынке). Тогда указанные соотношения баланса имеют вид:
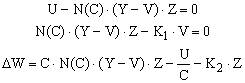 |
(1.2.1) |
Третье уравнение показывает, что доход в единицу времени складывается из выручки от продаж 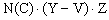 единиц товара по цене С, расходов на производство U и затрат на хранение K единиц товара по цене С, расходов на производство U и затрат на хранение K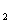 ; все величины измеряются в единицах времени. ; все величины измеряются в единицах времени.
В этой модели величины U, C, V, Z,  W - постоянны. Поскольку параметры U и C назначаются производителем, то он, естественно, желает выбрать их так, чтобы максимизировать доход W - постоянны. Поскольку параметры U и C назначаются производителем, то он, естественно, желает выбрать их так, чтобы максимизировать доход  W. W.
1.3 Построение динамических моделей
Под простейшей динамической системой обычно понимается система, поведение которой задается совокупностью обыкновенных дифференциальных уравнений в форме Коши с достаточно гладкими правыми частями, обеспечивающими существование и единственность решения. Решение систем уравнений в форме Коши, разрешенных относительно первых производных, - традиционная численная задача. Разработанные в последние годы программные реализации численных методов не только обеспечивают заданные требования к погрешности решения, но стараются самостоятельно определить тип (вычислительную сложность) решаемой задачи.
Более сложной является модель, представленная системой обыкновенных дифференциальных уравнений в форме Коши и нелинейных алгебраических уравнений, сопровождаемая набором вспомогательных формул. Задача численного построения фазовой траектории такой системы значительно сложнее, но если совокупность нелинейных уравнений однозначно разрешима в каждой временной точке, и правые части дифференциальных уравнений достаточно гладкие, то она в основном также вполне успешно решается. Предварительная подготовка для численного решения в данном случае минимальна: нужно проверить равно ли число уравнений числу неизвестных, проверить согласованность начальных условий и провести сортировку формул в правильном порядке (для замены их операторами присваивания).
Математическая модель, описывающая поведение простейшей динамической системы, называется динамической моделью.
1.3.1 Построение динамической нелинейной модели
Перейдём теперь к составлению динамической модели и её сопоставлением с моделью (1.2.1). Поскольку за время dt прирост произведённого товара равен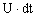 , а продаётся , а продаётся 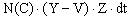 единиц товара, то скорость прироста товара на рынке равна единиц товара, то скорость прироста товара на рынке равна
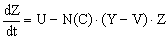 |
(1.3.1.1) |
Прирост dV товара у потребителя за время dt равен количеству dy проданного товара минус количество 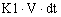 потреблённого товара: потреблённого товара:
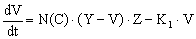 |
(1.3.1.2) |
Уравнения (1.3.1) и (1.3.2) совместно с расчётом дохода за единицу времени образуют динамическую модель:
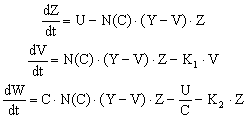 |
(1.3.1.3) |
Нетрудно заметить, что статическая модель (1.2.1) может быть получена из построенной динамической (1.3.3) приравниванием нулю правых частей первых двух уравнений в (1.3.3). Поэтому статическая модель может рассматриваться как частный случай динамической, отражающий состояние динамического равновесия последней, но динамическая модель гораздо "богаче" информацией об экономической системе, чем статическая.
1.3.2 Построение динамической линейной модели
При моделировании реальных процессов и проектировании цифровых систем часто используют линейные модели, так как они очень удобны в описании. К тому же очень хорошо развит аппарат анализа линейных моделей. В силу этого линеаризуем динамическую модель (1.3.1.3) и в дальнейшем будем работать именно с линейной моделью.
В общем случае линейный объект описывается следующим образом:
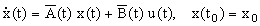 |
(1.3.2.1) |
где x - n - мерный вектор состояний, 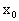 - вектор начальных условий, u - m - мерный вектор управления. - вектор начальных условий, u - m - мерный вектор управления.
Решим задачу Коши для системы линейных нестационарных дифференциальных уравнений (1.3.1.1). Несмотря на все разнообразие численных методов решения ЛДУ, определенный интерес, особенно в задачах реального времени, представляет использование метода Эйлера. Это объясняется сравнительно низкими вычислительными требованиями метода, а также тем обстоятельством, что переход к разностной модели с помощью метода Эйлера сохраняет размерность фазового пространства и порядок модели, что связано с вопросом сохранения физического смысла фазовых координат.
Численное решение на отрезке [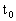 , ,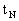 ] задачи Коши (1.3.2.1) ] задачи Коши (1.3.2.1)
состоит в построении таблицы приближенных значений
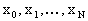 решения x(t) в узлах сетки решения x(t) в узлах сетки 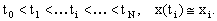 Если Если 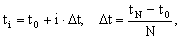 то сетка называется равномерной. то сетка называется равномерной.
Численный метод решения задачи Коши называется одношаговым, если для вычисления решения в точке 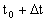 используется информация о решении только в точке используется информация о решении только в точке 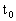 . Простейший одношаговый метод численного решения задачи Коши - метод Эйлера. В методе Эйлера величины . Простейший одношаговый метод численного решения задачи Коши - метод Эйлера. В методе Эйлера величины 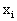 вычисляются по формуле вычисляются по формуле 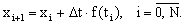 Отсюда: Отсюда:
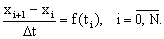 |
(1.3.2.2) |
Определим x, как вектор пространства состояний, компоненты которого являются параметрами динамической модели (1.3.1.3).
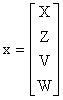 |
(1.3.2.3) |
где X=X(t) - объём производства продукции, Z=Z(t) - количество товара на рынке, V=V(t) - количество товара у потребителей (ещё не потреблённого), W=W(t) - доход (разница между выручкой и затратами на единицу времени). Сопоставив (1.3.2.1) с динамической моделью (1.3.1.3), найдём динамические матрицы влияний 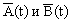 . .
1.3.3 Построение моделей рынка и потенциального спроса
Выражая V и Z из первых двух уравнений в (1.2.1) через U и C получим величину количества единиц товара у потребителей (ещё не потреблённого):
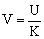 |
(1.3.3.1) |
Количество товара на рынке, также определим в соответствии с (1.3.2.1) в результате получим:
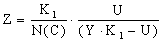 |
(1.3.3.2) |
Потенциальный спрос на ликёро - водочную продукцию в данной модели определяется, в соответствии с моделью рынка, как величина, превосходящая темп производства в среднем в 1,2 раза, увеличивающаяся к праздникам, а особенно - к "Новому Году".
1.3.4 Исходные данные и их аппроксимация
В качестве исходных данных даны суммы выручки от реализации продукции за месяц. Данные суммы представлены в виде вектора U, состоящего из 12 элементов (за год).
Рассматриваемый процесс имеет моменты пиков и спадов. Это объясняется тем что, производство нестабильно, так как в какой-то мере определяется потребностями клиентов, а значит, отражает колебания спроса. В связи с этим удобней будет работать с аппроксимированными параметрами модели.
Аппроксимацию выполним методом наименьших квадратов.
Пусть 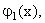 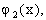 …, …, 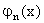 - последовательность линейно-независимых функций на [a,b]. Аппроксимирующую функцию - последовательность линейно-независимых функций на [a,b]. Аппроксимирующую функцию 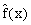 будем представлять в виде: будем представлять в виде:
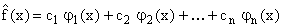 |
(1.3.4.1) |
где 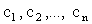 - неизвестные параметры. - неизвестные параметры.
Тогда, согласно методу наименьших квадратов, функционал J, имеющий смысл суммы квадратов отклонений функций 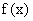 и и 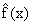 в заданных точках в заданных точках 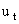 , , 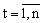 , запишется в виде: , запишется в виде:
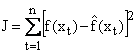 |
(1.3.4.2) |
и параметры 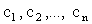 будем выбирать из условия минимума этого функционала, т.е. будем выбирать из условия минимума этого функционала, т.е.
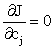 |
(1.3.4.3) |
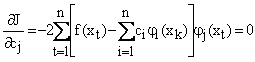 |
(1.3.4.4) |
или
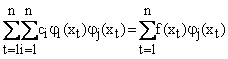 |
(1.3.4.5) |
Последнее выражение можно записать в виде системы линейных алгебраических уравнений относительно неизвестных параметров 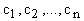 . .
 |
(1.3.4.6) |
или в матричной форме:
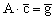 |
(1.3.4.7) |
где A - симметрическая матрица порядка n, 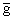 - n мерный вектор-столбец свободных членов, - n мерный вектор-столбец свободных членов, 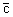 - n мерный вектор-столбец неизвестных параметров, т.е. - n мерный вектор-столбец неизвестных параметров, т.е.
 |
(1.3.4.8) |
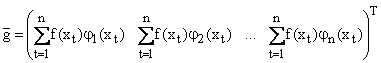 |
(1.3.4.9) |
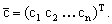 |
(1.3.4.10) |
Таким образом, задача нахождения параметров аппроксимирующей функции (1.3.3.1) свелась к решению системы линейных алгебраических уравнений (1.3.4.7) и в дальнейшем можно действовать двумя способами: либо искать решение системы (1.3.4.4), либо находить матрицу 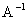 , обратную матрице A, тогда , обратную матрице A, тогда
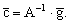 |
(1.3.4.11) |
В данном случае при аппроксимации удобно придерживаться второго пути. В качестве последовательности 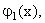 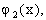 …, …, 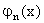 - взяты - взяты 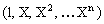 . Экспериментально получено, что для конкретных исходных данных наилучшей (в смысле среднеквадратического отклонения) будет аппроксимация полиномами 6-ой степени. . Экспериментально получено, что для конкретных исходных данных наилучшей (в смысле среднеквадратического отклонения) будет аппроксимация полиномами 6-ой степени.
|

