© Ф.Пинежанинов
К списку статей
Зеркало: http://pinega.da.ru/
Словарь русского языка определяет понятие прочности следующим
образом: "прочный - 1) крепкий, с трудом поддающийся разрушению, порче, 2) не
подверженный переменам, надежный, постоянный ".
Вопрос прочности - или
границы смены расчетных технологий принципиальны для механики сплошной среды и
ее фундамента: математической теории упругости, теории линейных задач, по
существу; математической теории пластичности, более обще - нелинейных гладких
задач; негладких задач имеющих разрывы производных по перемещениям, контактные
задачи и задачи с трещинами. На все это возможное поведение материала
естественно накладывается возможная зависимость от времени - динамические и
эволюционные задачи, удары, ползучесть, усталость, колебания.
Для того чтобы сравнивать различные математические объекты
одной природы, необходимо, исходя из некоторой логики, построить отображение на
числовую ось. Тогда возможно ввести понятие ближе - дальше или больше - меньше.
Другими словами определить функцию-норму от математического объекта для его
оценки. Например, для векторов это может быть длина вектора.
Введение нормы,
или другими словами руководящего правила, принципа оценки, породит понятие
эквивалентности, то есть одному и тому же числовому значению нормы будут
соответствовать различные математические объекты. Для трехмерных векторов,
наделенных нормой в виде длины вектора, например, возникнет множество
эквивалентных по норме объектов и это будет сфера. То есть когда мы говорим об
эквивалентности, то подразумеваем, все множество или сферу, на которой
располагаются всевозможные вектора с такой длиной.
Это не единственный
способ вводить функцию-норму, например, если мы идем на каяке по бурной реке, то
для того, чтобы оценить насколько мы продвинемся, сделав одинаковое число
гребков, совсем не безразлично в какую сторону мы движемся. Здесь есть
зависимость от направления и эквивалентная по затратам мускульной энергии
поверхность будет напоминать сечение воздушного шарика на ветру, удерживаемого
за ниточку.
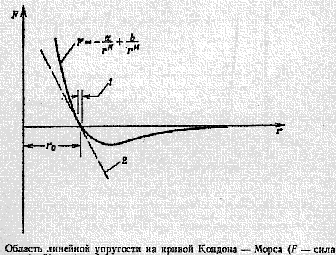
Из физики (кривые Кондона-Морса) известно, что силы межатомного
взаимодействия при отклонениях расстояния между атомами от равновесного
положения в большую сторону или растяжению уменьшаются по квадратичному закону,
а при отклонении в меньшую сторону или сжатию, растут по степенной функции
порядка 8. То есть, если внешняя сила приводит к увеличению расстояния, то по
мере его увеличения сопротивление изменению падает, и тогда, когда сопротивление
будет меньше растягивающих сил, система практически распадется на подсистемы.
При сжимающих усилиях ситуация обратная, чем сильнее сжимаем, тем больше растет
сопротивление и равновесие всегда соблюдается, а разрушения системы не будет.
Реальные тела состоят из разнородных по механическим свойствам
объектов, эту неоднородность всегда можно увидеть при том или ином увеличении.
Эта неоднородность свойств вызывает изменение напряжений при рассмотрении
небольших объемов даже при однородной нагрузке. Рассмотрим всестороннее сжатие,
при этом часть компонентов со слабыми свойствами к сопротивлению сожмутся
больше, чем более прочные компоненты, а это приведет к искажению геометрии, а
значит, с высокой вероятностью, где-то возникнут малые зоны растяжения и
возможно локальное разрушение, которое в свою очередь изменит геометрию и так
далее. Произойдет что-то похожее на потерю устойчивости сжатого стержня по
Эйлеру, в ситуации, когда сжатие плюс возмущения геометрии приводят к
растягивающим напряжениям. То есть разрушение будет происходить всегда, или
из-за растяжений или из-за вторичных растяжений, вызванных сжатием плюс
вероятностью несовершенства. Под разрушением обычно понимается разделение тела
на отдельные тела. Под прочностью обычно понимается, что изделие, при каком то
напряженно-деформированном состоянии способно выполнять свои функции без
разрушения. Таких состояний, естественно множество и нужен механизм их оценки.
Далеко ли до разрушения и насколько еще можно повышать нагрузку, а,
следовательно, каковы запасы прочности?
Нарушение прочности обычно
подразумевает замену или усиление объекта и связано с невозможностью
выполнять ожидаемые функции.
Другими словами необходимо ввести норму, которая позволяла бы
судить о прочности. Естественно для изотропных материалов эта норма не должна
зависеть от системы координат и, следовательно, должна записываться через
инварианты тензора напряжений или деформаций.
В процессе роста нагрузки
до разрушения можно выделить несколько стадий. При небольших нагрузках тело
обычно ведет себя упруго и связь между напряжениями и деформациями линейная и
определяется законом Гука. При дальнейшем росте нагрузки связь становится
нелинейной, но остается гладкой, этот момент перехода для одномерного случая
определяется пределом текучести. При этом в случае понижения нагрузки связь
между напряжениями и деформациями снова становится линейной. Поэтому этот
процесс по аналогии поведения иногда связывают с трением двух тел, но при этом
говорят о внутреннем трении в материале. При дальнейшем росте нагрузки возникают
нарушения гладкости связи напряжений и деформаций, обычно предельное
состояние для этого случая определяются пределом прочности, из-за
нарушения гладкости можем говорить о трещинах, или разрыхлении. Далее процесс
связан с увеличением разрывов в производных и заканчивается полной
независимостью напряжений от деформаций или разрушением. Первые две стадии носят
достаточно локальный характер, а третья стадия обычно охватывает уже все
деформируемое тело. Таков обычно математический взгляд на разрушение.
Для
независимости от систем координат поверхность разрушения должна быть функцией
инвариантов тензора напряжений.
Поскольку все начинается с поверхности, а
там двумерное напряженное состояние, обычно хватает двух инвариантов тензора
напряжений для построения теорий прочности. Предельные поверхности в
пространстве напряжений, на которых осуществляется переход с линейных
соотношений на гладкие, а затем и с гладких соотношений на разрывные соотношения
между напряжениями и деформациями, строятся в двухмерном
пространстве. Для описания внутренних областей обычно
используют аналитическое продолжение, а не привлекают третий инвариант. Такова
традиция. Наиболее удобные инварианты предложил Мор - σ,τ - сжатие и сдвиг,
определяемые через шаровую часть и девиаторную часть тензора. Переход от одной
стадии к другой описывается кривыми τ(σ) , а продолжение на трехмерное
пространство главных напряжений в силу изотропии материала осуществляется
вращением кривой вокруг оси, связанной с гидростатическим сжатием.
Вектор обладает одним инвариантом, то есть величиной, не
зависящей от системы координат - длиной. Тензор второй валентности иногда можно
рассматривать как матрицу, то есть вектор из векторов, поэтому, как доказывается
в алгебре, тензор второй валентности в трехмерном пространстве, обычно
используемый для описания напряжений или деформаций в механике, имеет три
независимых инварианта.
Но различных троек инвариантов может быть много и
всегда можно одну группу инвариантов тензора выразить через
другую.
Двухвалентные тензоры имеют представление квадратными матрицами, а
они, рассматриваемые как линейные операторы, естественно имеют собственные
числа. В механике эти собственные числа двухвалентного тензора имеют название
главных напряжений или деформаций. В алгебре показывается, что они не зависят от
системы координат, то есть являются инвариантами тензора и в определенной
системе координат, определяемой собственными векторами, согласованными с
собственными числами, все недиагональные элементы тензора нулевые. То есть в
системе координат, определяемой собственными векторами, главные напряжения можно
рассматривать как координаты трехмерного вектора, полностью определяющего тензор
напряжений.
А это уже можно рисовать и использовать геометрическую
интуицию.
В дальнейшем для удобства под трехмерной системой координат будет
пониматься система, связанная с главными векторами, а под тензором вектор в ней
с координатами главными напряжениями. Условие равномерного сжатия - растяжения
или равенства всех компонент вектора порождает в этой системе координат ось,
называемую обычно гидростатической осью, по аналогии с давлением в гидростатике
или иногда говорят о среднем нормальном к площадкам кубика
напряжении.
Интуитивно понятно, и можно строго показать алгебраическими
методами, что среднее давление на кубик не будет зависеть от ориентации этого
кубика, другими словами среднее нормальное напряжение является инвариантом
тензора напряжений. Аналогично и для деформаций - среднее изменение объема
кубика не должно зависеть от системы координат.
Аналогичный результат можно получить и для касательных
напряжений: так Новожилов показал, что среднеквадратичное касательное напряжение
для малой сферы пропорционально максимальному касательному напряжению, это, в
общем, и естественно: одну систему инвариантов тензора можно выразить через
другую.
Будем рассматривать изотропный материал, то есть подразумевать,
что свойства материала во всех направлениях одинаковые, а это значит, что любой
вектор, повернутый вокруг этой оси, будет неразличим по свойствам с исходным
вектором. То есть поверхность разрушения должна быть симметричной относительно
гидростатической оси и ситуацию можно еще упростить и использовать для описания
поверхности двухмерное пространство. Для этого определим плоскость как
проходящую через гидростатическую ось и один из собственных векторов тензора.
Горизонтальную ось совместим с гидростатической осью, а вертикальную, следуя
Мору, проведем через начало координат ортогонально ей.
К вопросу о
названии приведу цитату из книги Биргера "Критерии прочности в курсах
сопротивления материалов было принято называть теориями прочности. Такое
название нельзя признать удачным, так как теоретические обоснования критериев
прочности невелики. Их следует считать разумными обобщениями экспериментальных
данных".
Ну, что делать, закон всемирного тяготения, да и вся рациональная
наука всего лишь РАЗУМНОЕ обобщение экспериментальных данных, этим и будем
заниматься, а математика наиболее совершенный и внутренне непротиворечивый
инструмент РАЗУМА. Именно поэтому Делез считает теорию легитимнее
эксперимента.
С другой стороны изотропные материалы можно рассматривать
как сложные хаотично организованные системы, для которых справедливы
синергетические представления- "обращение к анализу поведения элементов
микроуровня системы также не может дать искомого результата, ибо новое состояние
системы возникает как непредсказуемый системный эффект". По крайней мере такой
вывод можно сделать из статьи о неодетерминизме из "Всемирной энциклопедии
философии XX века".
Для двухвалентных тензоров в декартовой системе координат
возможно матричное представление, поэтому, когда говорим о тензоре в рамках
данной статьи, можно понимать и квадратную матрицу 3*3. Основные определения
приведу, опираясь на любимую книгу по механике деформируемой среды
Фомина.
Тензор напряжений, равный метрическому тензору (единичной матрице в
нашем случае) с точностью до скалярного множителя, называется шаровым.
След
тензора T (или двойная свертка | линейный инвариант | первый инвариант | Sp T) -
для матричного представления - сумма диагональных элементов, в механике имеет
смысл утроенного гидростатического давления. Если вычтем из тензора его шаровой
тензор, то получим объект известный как девиаторная часть тензора или просто
девиатор тензора. Другими словами всегда существует разложение тензора на
шаровую компоненту и девиаторную компоненту.
Приведем некоторые полезные
соотношения между различными системами инвариантов:

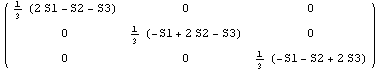 и 0. и 0.

0
Нулевой результат сравнения говорит о тождестве сравниваемых
величин. Как обычно, сравнения проводились в символической форме, следовательно,
верны всегда.
Ввиду важности, еще раз вспомним результат Новожилова о
среднем нормальном напряжении как гидростатическом давлении и о
среднем касательном напряжении как линейной функции от 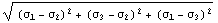 ,
то есть от корня из утроенного следа квадрата девиатора и о связи его с
максимальным касательным напряжением ,
то есть от корня из утроенного следа квадрата девиатора и о связи его с
максимальным касательным напряжением  . .
Как отмечалось ранее, тензор
удобно изображать геометрически в трехмерном декартовом пространстве
главных напряжений. В этом случае, каждый тензор
может быть представлен как трехмерный вектор.
Возьмем ранее полученные значения для девиаторной и шаровой
компонент тензора в виде векторов и вычислим их скалярное
произведение:

{{0}}.
Нулевой результат говорит об ортогональности шаровой и
девиаторной части тензора, представленных как
вектора в пространстве главных напряжений.
Так как главные значения, или
собственные числа матрицы, являются инвариантами,
то есть не зависят от системы координат, то и любые комбинации из них будут
инвариантами.
Поэтому, следуя традиции заложенной Кулоном и Мором, выберем в качестве двух инвариантов:
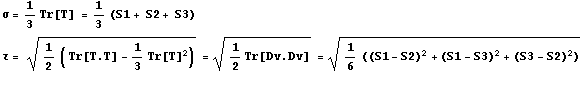
Следуя Филоненко-Бородичу, будем считать все теории прочности,
задающие зависимость τ(σ), как обобщения теории Мора.
В пространстве
главных напряжений шаровым частям тензора будет соответствовать линия, одинаково
наклоненная к координатным осям и, в силу ортогональности, девиаторам будет
соответствовать плоскость ортогональная этой линии. В силу определения и линия и
плоскость будут проходить через начало координат и, следовательно, будут
определяться вектором
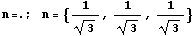
Каждому напряженному состоянию в двухмерном пространстве
инвариантов (σ, τ) будет соответствовать точка на плоскости. Если в
трехмерном пространстве главных напряжений известна некоторая точка,
соответствующая тензору, то всегда можем вычислить ее проекцию на
гидростатическую ось через скалярное произведение на вектор n. С другой стороны
через это же скалярное произведение можем определить угол между вектором n и
вектором напряженного состояния 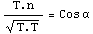 , а,
следовательно, и нанести точку на плоскость (σ, τ), или нарисовать направление,
на котором будут находиться все точки для напряженного состояния определенного с
точностью до величины приложенного усилия. , а,
следовательно, и нанести точку на плоскость (σ, τ), или нарисовать направление,
на котором будут находиться все точки для напряженного состояния определенного с
точностью до величины приложенного усилия.
Рассмотрим, какие значения принимают эти инварианты при
некоторых напряженных состояниях, которые позволяют однозначно судить о
напряжениях:

Одномерное напряженное состояние - растяжение тонкого стержня
 => =>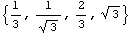 и и 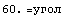
Одномерное напряженное состояние - сжатие тонкого стержня
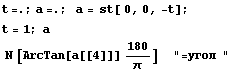 => =>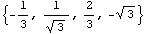 и и 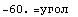 . .
Двухмерное напряженное состояние - растяжение тонкой пластинки
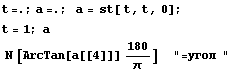 => =>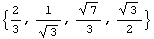 и и 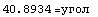
Двухмерное напряженное состояние - сжатие тонкой пластинки
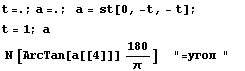 => =>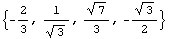 и и 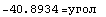
Двухмерное напряженное состояние - кручение тонкого
цилиндра или чистый сдвиг
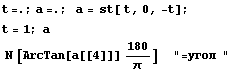 => =>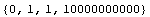 и и 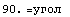
Трехмерное сжатие - смятие в инженерных науках
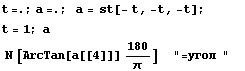 => =>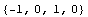 и и 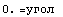
Трехмерное растяжение
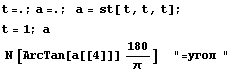 => =>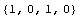 и и 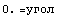
Построим диаграмму направлений в системе координат Кулона-Мора
(σ,τ) с единичными векторами.

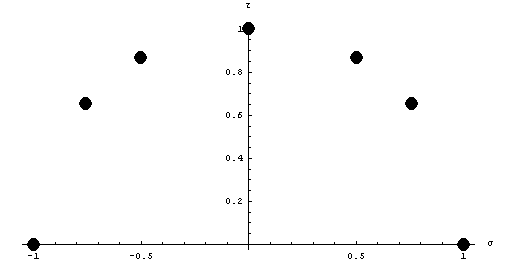
Таким образом, если известны из экспериментов длины векторов
проходящих через эти точки, то можем строить различные аппроксимации образующей
поверхности текучести или разрушения, опираясь на мнение Биргера, что теории
прочности это по существу обобщение экспериментальных данных.
Простейшие и
широко используемые функции - полиномы, при этом количество минимально
необходимой информации определяется порядком полинома.
Рассмотрим разложение
в ряд Тейлора в окрестности нуля предельной кривой τ(σ) , то есть такой кривой,
на которой происходит качественное изменение поведения материала:
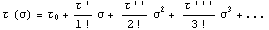
Это разложение можно осуществить и в безразмерном
виде

Так как в этом случае производные безразмерные, то, следуя
аналогии им можно придать тригонометрический смысл тангенса некоторого угла:
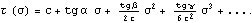
В таком виде предельную поверхность уже можно наделить обычным
физическим смыслом.
Если рассмотреть случай нулевого порядка τ(σ)=c, то получим
классический критерий прочности Мизеса. Здесь надо определить одну константу
материала достаточно провести один опыт, а если известно много разных, то,
используя метод наименьших квадратов, или какой-нибудь другой принцип осреднения
можно свести к одной константе. Аналогично надо поступать в случае любой
избыточной информации. Если это выражение умножить на 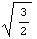 ,
то можно говорить о напряжении эквивалентному растяжению стержня, как это
следует из приведенных выше вычислений, это и предложил Мизес использовать в
качестве критерия прочности, носящего его имя. ,
то можно говорить о напряжении эквивалентному растяжению стержня, как это
следует из приведенных выше вычислений, это и предложил Мизес использовать в
качестве критерия прочности, носящего его имя.
Если рассмотреть аппроксимацию первого порядка τ(σ)=c-tg α
σ, то получим выражение известное как закон Кулона, где -c - обычно называют
сцеплением грунта, а 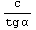 сжатием
эквивалентным связности материала, или можно трактовать c как трехмерное
растяжение, приводящее к разрыхлению или полному разрушению материала. Величину
-α называют углом внутреннего трения материала, чтобы подчеркнуть сходство
пластического деформирования с сухим трением в аналитической механике. сжатием
эквивалентным связности материала, или можно трактовать c как трехмерное
растяжение, приводящее к разрыхлению или полному разрушению материала. Величину
-α называют углом внутреннего трения материала, чтобы подчеркнуть сходство
пластического деформирования с сухим трением в аналитической механике.
Конус, который возникает в пространстве главных напряжений при
вращении этой образующей при вращении вокруг гидростатической оси, обычно
связывают с именами Друкера и Прагера.
Квадратичная аппроксимация 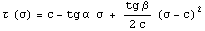 позволяет
загибать прямую линию образующей вверх или вниз в зависимости от знака угла
β. позволяет
загибать прямую линию образующей вверх или вниз в зависимости от знака угла
β.
Было предложено несколько других видов квадратичных аппроксимаций, но они
не нашли применения в практике современных вычислений.
Кубичная аппроксимация представляется наиболее интересной по
сравнению с предыдущими, так как позволяет строить гладкие и несимметричные
образующие, охватывающие несколько точек аппроксимации. Для ее описания
достаточно знать длины четырех из семи векторов, однозначность определения
остальных обеспечит теорема о единственности интерполирующего полинома.
При
необходимости естественно имеется возможность строить кусочно-гладкие
интерполяции, но эти варианты ввиду их тривиальности не будем рассматривать,
кроме того, они требуют определения всех семи точек, что обычно проблематично в
простейших экспериментах, и, следовательно, требуется принятие различных
гипотез, что естественно снижает общность.
Статистический анализ данных о
сталях, представленных в известном справочнике Анурьева, приводит к следующим
соотношениям для допускаемых напряжений:
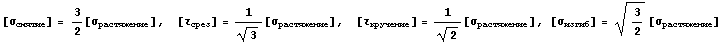
Разумно предполагая, что во всех случаях предусмотрены
одинаковые коэффициенты запаса, кроме того, это справочник для машиностроителей,
где критичным обычно считается наступление пластического течения, можем принять,
что эти точки описывают образующую поверхности наступления текучести для сталей.
Кроме того, кручение и срез имеют примерно одинаковые напряженные состояния, как
и растяжение и изгиб (естественно в смысле координат σ-τ), можно считать, что в
трех направлениях величины нам известны: смятие, кручение и одномерное
растяжение.
Ландау и Лившиц в "Теории упругости" дают для деформаций
следующие понятия: "деформации без изменения объема называют сдвигом", и "всякую
деформацию можно представить в виде деформации чистого сдвига и всестороннего
сжатия". Если прейти на напряжения, то и получим два инварианта связанные с σ и
τ.
Как замечание к статистической обработке данных из справочника
Анурьева отметим еще полезные полученные соотношения:
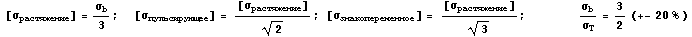
Для всех соотношений точность не менее 10%, за исключением
последнего, приведенного скорее для качественной оценки. В квадратных скобках,
как обычно указаны допускаемые значения напряжений. Учитывая, что
Филоненко-Бородич оценивает максимальную точность теорий прочности на уровне
15%, приведенные соотношения в силу статистической независимости с оценкой для
теорий прочности можно считать приемлемыми для большинства приложений.
Кроме
того полезна оценка точности кривых деформирования, приведенная Хиллом "кривые
для какого-нибудь одного металла, полученные различными путями, могут
различаться приблизительно на 10%" , то есть формулы дают вполне приемлемый
результат.
Внимательно посмотрев на картинку с экспериментами из книги
Коллинза,
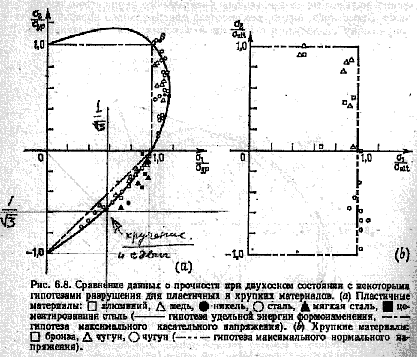
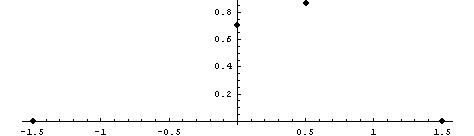
можно сделать вывод, что предельное состояние при предельном
двухмерном растяжении чуть больше предельного одномерного растяжения, поэтому
учтем, что в условиях всестороннего растяжения все материалы ведут себя хрупко и
примем, как советует Биргер, в качестве предельного значения сигма временное,
которое по данным из справочника Анурьева порядка 3/2 сигма текучести. При
наличии более точных данных всегда можно учесть коэффициентом. То есть можно
считать определенной и четвертую точку, всестороннего растяжения, как равную
одномерному растяжению по длине вектора.

В силу теоремы о единственности интерполирующего полинома
общность не снижается, если
для интерполяций будем использовать обычную
конечноэлементную технику построения кубичных базисных функций:

1.0535
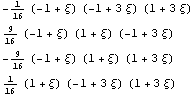
1
В векторе Bn находятся базисные функции и обычным, для метода
конечных элементов, образом можем построить гладкую кубичную интерполяцию для
образующей поверхности начала текучести:

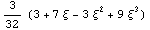
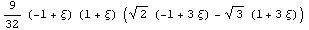
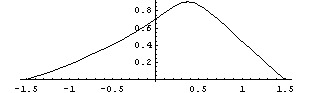
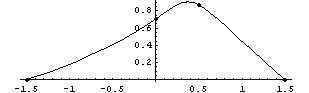
Осуществив вращение образующей вокруг девиаторной оси, и
повернув два раза вокруг осей пространства главных напряжений несложно получить
изображение поверхности текучести в трехмерном пространстве главных напряжений.
В правом верхнем углу область растяжений.
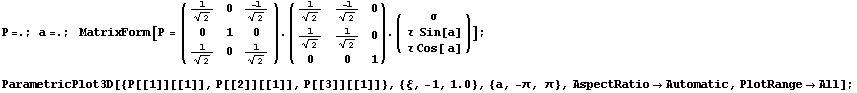
Наблюдаемая на некоторых участках вогнутость вступает в
противоречие с постулатом Друкера, но ведь материал и должен оказаться в
неустойчивом состоянии, чтобы иметь возможность осуществлять структурные
изменения, которые проявятся в виде пластического течения.
Для хрупких материалов обычно приводят 2 характеристики -
предельное одномерное растяжение и предельное одномерное сжатие, при которых
происходит разрушение. Из рассмотрения правого графика рисунка из книги Коллинза
можно сделать логичное предположение о том, что величина предельного значения
для двумерного растяжения совпадает с соответствующим значением для одномерного.
Хрупкие материалы характерны тем, что предел упругости практически совпадает с
пределом прочности, то есть сдвиги атомных слоев или движение дислокаций
практически сразу приводят к образованию микротрещин их развитию и хрупкому
разрушению.
Можно предположить, что при сжатии хрупкие материалы,
образованные из достаточно крупных частиц ведут себя одинаково при одномерном,
двухмерном и трехмерном сжатии.
В пользу такого предположения можно привести
высказывание из книги Филоненко-Бородича: "В другой серии опытов А.Феппль
подвергал кубики из камней и цемента испытанию на сжатие в одном и в двух
взаимно-перпендикулярных направлениях ... опыты систематически показывали
одинаковую прочность". Посмотрев на ранее вычисленные длины векторов в
двухмерном σ-τ пространстве Мора при однородных напряженных состояниях в рамках
упругости можем считать, что в долях одномерного сжатия двумерное сжатие
составляет
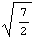 , а
трехмерное сжатие , а
трехмерное сжатие 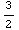 .
Таким образом, имеем 4 значения и можем построить образующую поверхности
разрушения. .
Таким образом, имеем 4 значения и можем построить образующую поверхности
разрушения.
Для бетона, например, отношение одномерного растяжения к
одномерному сжатию где-то в диапазоне 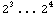 . .

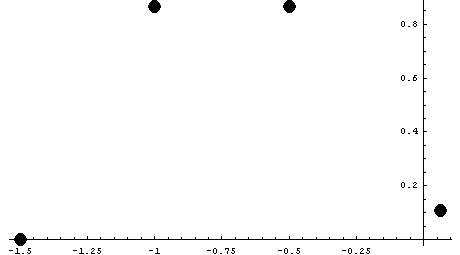

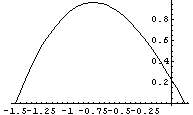
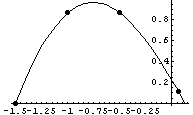
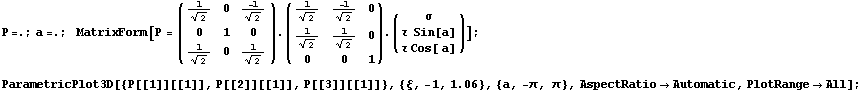
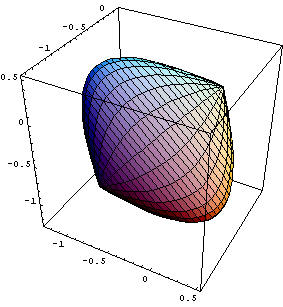
Теперь для другого крайнего отношения:

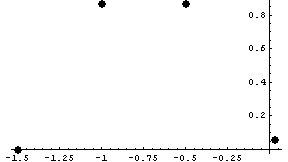

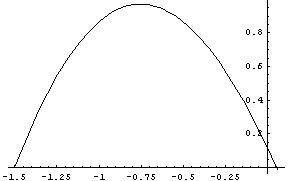
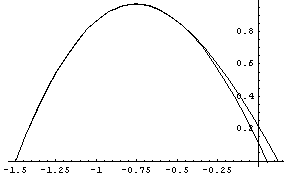
Сравнение двух кривых показывает, что кривые практически
совпадают в рабочих областях использования бетона в зоне сжатия.
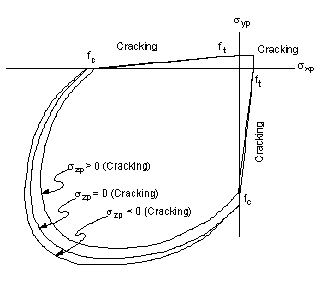
В Ansys для моделирования бетона сечение поверхности разрушения
выглядит так, что предельное трехмерное сжатие примерно в 2 раза больше
предельного одномерного.
Точнее рекомендуется предельное гидростатическое
сжатие как 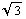 из предельного одномерного сжатия. Из
внимательного рассмотрения можем сделать вывод о достаточно хорошем совпадении с
ранее описанным случаем, расхождение порядка 15%. из предельного одномерного сжатия. Из
внимательного рассмотрения можем сделать вывод о достаточно хорошем совпадении с
ранее описанным случаем, расхождение порядка 15%.
В литературе по
экспериментам с железобетоном приводятся предельные значения деформаций для
сжатия порядка 0.003...0.005, то есть разброс результатов намного больше
расхождения в теоретических моделях.
Гладкость в области сжатия в рамках
кубичной модели может быть только случайной или надо отказаться от одного из
использованных значений, заменив его бесконечным значение производной в области
трехмерного сжатия.
Но в практических вычислениях такая точность
моделирования поведения материала не всегда удобна, так как не позволяет
использовать простые краевые условия типа шарнирных опор, а требует точного
моделирования в областях контакта. Для преодоления этой избыточной, в данной
ситуации точности, для моделирования в области краевых условий удобно
использовать материал с линейной или квадратичной точностью интерполяций
поверхности разрушения типа Друкера-Прагера. А вне этих областей для обнаружения
трещинообразования следует переходить на интерполяцию поверхности кубическими
кривыми.
В хрупком разрушении есть еще один интересный вопрос, как
будет ориентирована зародившаяся по достижении предела прочности трещина. Тысячи
наклеенных и обработанных тензодатчиков, и нанесенных лаковых покрытий на
разнообразные детали во время работы на Кировском заводе однозначно убедили
автора в том, что трещина всегда ориентируется ортогонально другому инварианту
тензора - первому главному напряжению, или другими словами, трещина лежит в
плоскости двух других главных напряжений тензора.
Для бетона, например,
принято, что трещины начинают образовываться при деформациях порядка 0.00015.
Поэтому для железобетона как деформационный критерий прочности часто используют
величину раскрытия трещины, как достаточно легко измеримый параметр с одной
стороны, и легко вычислимый при известных деформациях с другой.
Если материал идеально пластичный, то по достижению поверхности
текучести можно считать, что дальше он течет без разрушения примерно как очень
вязкая жидкость, при этом его способность сопротивляться зафиксирована
поверхностью текучести и в случае снятия нагрузки именно эта запасенная энергия,
освободившись, определит форму тела. Примерно как движение щетки по дивану,
после снятия нагрузки вызывающей движение, относительное положение щетки
определится упруго согнутыми волосками. Физически пластичность связывают с
проскальзыванием атомных плоскостей кристаллов и описывают в терминах дислокаций
(смещений), но обсуждение на качественном уровне выходит за рамки механических
представлений, и не будет рассматриваться здесь. Поэтому пластичность обычно
связывают с внутренним трением и по аналогии, поверхность наступления
пластичности описывают углом внутреннего трения и усилием необходимым для его
начала, как это делал Кулон. В любой ситуации пластичность связана с энергией
избыточной по отношению к возможности тела накапливать энергию. Так, например,
обратный процесс, отъем избыточной энергии охлаждением превращает жидкость в
твердое тело.
Если материал идеально хрупкий, то упругая энергия копится в
теле до полного разрушения и если потом сложить обломки, то они внешне
восстановят начальную форму тела, так разбитая в ресторане рюмка может быть
склеена жевательной резинкой, если не хочется платить за нанесенный заведению
ущерб. Могут и не заметить, если быстро уйти. А логику всегда можно подогнать
под потребности, например с десертом припозднились. В общем, все по басне
Крылова.
Реальные материалы редко ведут себя как экстремисты "все или
ничего", чаще всего существует значительная область компромисса между текучестью
и началом разрушения или изломов производных от перемещений или началом
трещинообразования. Приведем рисунок из книги под редакцией Серенсена:
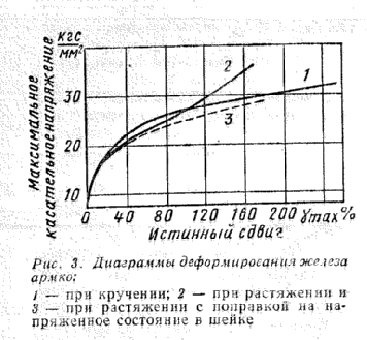
Из этого рисунка следует, что в отличие от текучести,
разрушение происходит при напряжениях кручения больших, чем одномерное
растяжение. Видимо сказывается возможность при сдвиге части атомов вступать в
новые устойчивые связи, как это происходит в жидкостях, в отличие от растяжения,
когда при увеличении расстояния просто происходит разрыв, как это предсказывают
кривые Кондона-Морса. С другой стороны при всестороннем растяжении разрыв будет
происходить, поэтому можем принять с некоторым запасом по прочности, что длины
векторов при начале трещинообразования при кручении, одномерном, двухмерном и
трехмерном растяжении примерно одинаковы и равны пределу прочности.

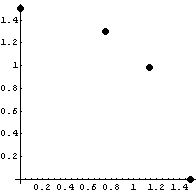

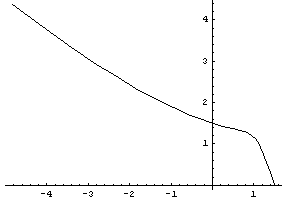
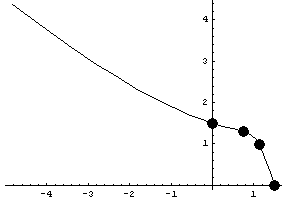
Нарисуем эту кривую в пространстве главных напряжений:
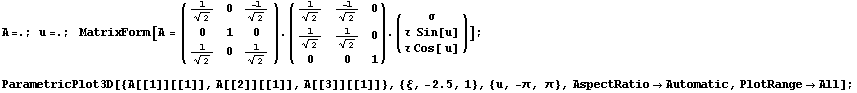
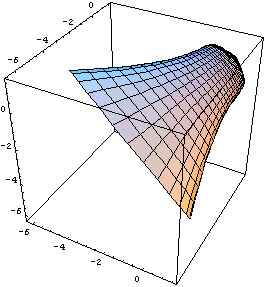
Рассмотрим линию одномерного нагружения.
Нарисуем совместно
для пластического металла образующую для поверхности текучести и поверхности
разрушения, вместе с направлением одномерного растяжения:

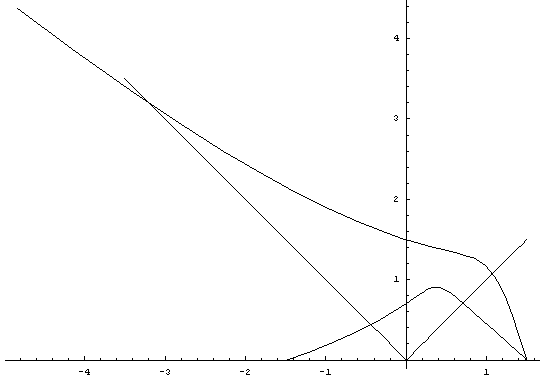
Итак, можем построить линию текучести
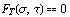 и линию
разрушения и линию
разрушения
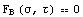 в плоскости инвариантов Мора. Как неоднократно делалось выше,
практически линии описываются параметрически, в зависимости от параметра,
изменяющегося в диапазоне порядка (-1 , 1) , так как интересуют только значения
с положительным инвариантом tay. в плоскости инвариантов Мора. Как неоднократно делалось выше,
практически линии описываются параметрически, в зависимости от параметра,
изменяющегося в диапазоне порядка (-1 , 1) , так как интересуют только значения
с положительным инвариантом tay.
Большинство
материалов обладает свойством упрочнения - типичным примером синергетического
поведения больших систем, когда малые эффекты приводят к макроскопическим
изменениям поведения, в данном случае к повышению предела упругости, как
способности накапливать энергию без необратимых изменений. Но возможности такого
приспособления ограничены и не ведут к повышению прочности. Здесь видимо
работает закон Гиббса: если поступившая энергия фиксирована, то энтропия
стремится к максимуму, а он согласован с наилучшей приспособляемостью к внешнему
воздействию. На атомном уровне это описывается как процесс смещения атомных
плоскостей (дислокаций) и возрастание их количества. В результате этого упругая
энергия связей размазывается по большим объемам и прочность повышается, примерно
так, как коэффициент концентрации единичного отверстия снижается, если число
отверстий в его окрестности увеличивается.
Но модуль упругости, как
величина, характеризующая межатомные связи, естественно не изменяется.
Таким
образом, разгрузка и последующая нагрузка пойдут уже по упругому, то есть без
необратимых изменений, пути.
Из-за свойства упрочнения материала актуальная
линия текучести будет изменяться. Если нагрузка, следовательно, и инварианты
тензора напряжений растут, то актуальная линия текучести будет располагаться
между двумя начальными кривыми, а если надо учесть эффект Баушингера,
заключающийся в снижении предела текучести на сжатие при растяжении и наоборот,
то актуальная кривая текучести будет ниже начальной для противоположной
нагрузки. Для этого часто используют тензор S , корректирующий реальный тензор
напряжений на основе информации о предыдущих воздействиях. При этом принимается,
что поверхность текучести не изменяется и определяется выражением F(σ-S)=0, что
эквивалентно  . В качестве дополнительной гипотезы
принимается зависимость S от предыдущего напряженного состояния. При таком
подходе называемом трансляционным упрочнением не удается согласовать поверхность
текучести и поверхность разрушения. . В качестве дополнительной гипотезы
принимается зависимость S от предыдущего напряженного состояния. При таком
подходе называемом трансляционным упрочнением не удается согласовать поверхность
текучести и поверхность разрушения.
Возможен и другой подход, при котором по мере роста
нагрузки плавно трансформируется поверхность текучести в поверхность разрушения,
при которой начинается образование микротрещин, а затем по мере роста нагрузки
снижается поверхность разрушения вместе с поверхностью текучести. При этом уже
можно говорить о хрупком поведении материала, так как из-за микротрещин
определяющим будет поведение материала в области микро концентраторов
напряжений, где наиболее опасным будет трехмерное напряженное состояние.
Для
учета эффекта Баушингера можно ввести кососимметричную функцию ортонормированную
на предельное гидростатическое сжатие и растяжение и имеющую скачек в области
чистого сдвига. Тогда если в области растяжений в координатах Мора кривая
текучести возрастает, то в области сжатий она будет уменьшаться. Это позволит
избавиться от мало реалистичного изменения предельных величин гидростатического
сжатия и растяжения при модели трансляционного упрочнения.
Эффект Баушингера обычно связывают с остаточными
напряжениями в наиболее деформированных зернах металла, которые, складываясь с
рабочими напряжениями приводят к снижению предела текучести при изменении знака
нагрузки.
Пусть мы имеем исходную поверхность
текучести и упрочненную поверхность текучести, описанные в виде заданных точек
для интерполяционного полинома, то всегда можем находить их разность. Значит, и
строить еще поверхность противоположной нагрузки как центрально
симметричную относительно исходной поверхности в том или ином смысле, например,
считая, что эффект Баушингера реализуется с весовыми коэффициентами по косинусу
угла с девиаторной осью и нормирующим множителем для растяжения-сжатия. В
принципе из экспериментов может быть подобрана любая подходящая функция
симметризации.
Например, можно потребовать, чтобы суммарная длина векторов
симметричных напряженных состояний по гидростатическому давлению (или
относительно девиаторной плоскости) имела одну и ту же длину, или ее проекцию на
девиаторную плоскость. При этом следует учесть, что, в рамках кубичной модели
образующей поверхности текучести, для однозначного описания линии надо
использовать 4 точки. Поэтому, хотя при построении начальной поверхности можно
использовать любые точки, в последующем по мере роста нагрузки лучше применять
одно и двух мерные сжатия и растяжения. И если гидростатическое давление
положительно, то еще раз вычислить одно и двухмерные растяжения с учетом
упрочнения, а одно и двухмерные сжатия вычислить из логики учета эффекта
Баушингера, то есть скорректировать длины соответствующих векторов. То есть
вычислять две поверхности разрушения и в зависимости от знака гидростатического
давления выбирать то или иную ветку.
Практически, достаточно иметь базовое описание
кривой и коэффициент со знаком указывающим знак гидростатического давления от
предыдущей нагрузки. Сравнивая с текущим всегда можно выбрать ветку.
Рассмотрим линию одномерной нагрузки. Для нее будем считать
известными истинные пределы текучести и прочности при монотонном росте нагрузки.
Истинные, то есть отнесенные к реальному сечению, потому, что во времена
цифровой фотографии говорить о сложностях экспериментального измерения изменения
диаметров в процессе роста нагрузки смешно. В силу положительной определенности
энергии, как это показано, например, у Ландау и Лифшица в "Теории упругости"
модуль упругости должен быть неотрицательной величиной, а так как решение
упругопластических задач реализуется через последовательность из упругих задач,
то требование положительности модуля распространяется и на пластическую область.
То есть, обычно имеем кривую, связывающую напряжения и деформации в одномерном
случае.
Для произвольной нагрузки естественно предположить, что связь
напряжений и деформаций будет в некотором смысле пропорциональна одномерной
ситуации.
Пусть имеем конкретное напряженное состояние. Значит, в координатах
Мора имеем конкретное направление, задаваемое линией, подобно одномерному или
двухмерному состоянию.
Следовательно, можем определить точки пересечения с
линиями текучести и разрушения. Пусть длины соответствующих векторов 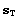 и и 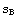 , а
длина вектора конкретной нагрузки - s. Тогда условие пропорциональности
одномерному случаю можно записать , а
длина вектора конкретной нагрузки - s. Тогда условие пропорциональности
одномерному случаю можно записать 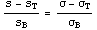 , где сигма
соответствует одномерному случаю. В ситуации, когда поверхность разрушения
пропорциональна поверхности текучести, приходим к гипотезе единой кривой. Введя
обозначение , где сигма
соответствует одномерному случаю. В ситуации, когда поверхность разрушения
пропорциональна поверхности текучести, приходим к гипотезе единой кривой. Введя
обозначение 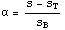 - параметр нагрузки, можем по его значению судить
о текущем упрочнении. Если α=0, то материал не упрочнен, если - параметр нагрузки, можем по его значению судить
о текущем упрочнении. Если α=0, то материал не упрочнен, если 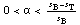 , материал находится в упрочненном состоянии, или
наклепан. Если α≤0 , то материал находится в упругом состоянии. , материал находится в упрочненном состоянии, или
наклепан. Если α≤0 , то материал находится в упругом состоянии.
Интересная
возможность возникает при введении понятия о текущем пределе текучести и
прочности. То есть, при последовательном росте и снижении нагрузки можем
менять
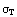 , а по
достижению , а по
достижению
 и продолжению увеличения нагрузки можем считать, что в этой
области деформируемого тела дислокаций уже настолько много, что они начинают
сливаться в микротрещины и и продолжению увеличения нагрузки можем считать, что в этой
области деформируемого тела дислокаций уже настолько много, что они начинают
сливаться в микротрещины и
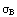 начинает снижаться вместе с ростом микротрещин. Как отмечает
Работнов: "Существуют материалы, деформирование которых сопровождается
появлением внутренних дефектов, что эквивалентно уменьшению площади
эффективного, т.е. несущего фактически нагрузку, сечения". начинает снижаться вместе с ростом микротрещин. Как отмечает
Работнов: "Существуют материалы, деформирование которых сопровождается
появлением внутренних дефектов, что эквивалентно уменьшению площади
эффективного, т.е. несущего фактически нагрузку, сечения".
При этом
разрушение будет продолжаться уже из-за концентрации напряжений, а совпадение
пределов текучести и прочности говорит о хрупком поведении в этой стадии.
В
общем, начинается шизоанализ, но еще в рамках непрерывных функций.
Под пластичностью обычно понимается свойство твердых тел
необратимо деформироваться под действием нагрузок. В теории пластичности обычно
рассматриваются деформации, не зависящие от времени. Всегда предполагается, что
существует предел упругости, и если напряжения ниже предела, то материал
находится в упругом состоянии, а если на пределе текучести, то к упругим
деформациям добавляются пластические деформации. Обычно предел упругости зависит
от предшествующих деформаций, при этом подразумевается, что нагрузка медленно
меняется.
Используя разложение тензора напряжений на шаровую часть и
девиаторную часть, можем записать 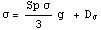 . .
При пластической деформации
обычно изменяется форма, а не объем, поэтому логично принимается, что приращения
пластической деформации зависят только от девиатора тензора напряжений, это
подтверждают и многочисленные эксперименты, то есть 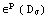 . .
Разложим пластическую деформацию
в ряд Тейлора в окрестности 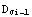 и
ограничимся линейным членом и
ограничимся линейным членом 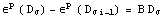 . .
Проведя анализ эквивалентный тому, который проводится для
изотропных материалов в теории упругости, получим, что могут быть только 2
независимых параметра у коэффициентов 4 валентного тензора B, а если учтем еще, что объем не меняется из-за пластического
деформирования, то останется всего одна компонента. Можно показать, что
приращения пластических деформаций пропорциональны девиатору напряжений 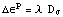 . Определить число необходимых констант можно и иначе.
Работа внешних сил величина не отрицательная и зависит от нагрузок. От нагрузок
зависят и напряжения. В условиях монотонного роста нагрузки есть однозначная
зависимость между нагрузками и напряжениями, следовательно, можно обратить и
формально считать, что работа зависит от напряжений, а в системе главных
координат от главных напряжений. Они являются инвариантами тензора и могут быть
заменены любыми другими инвариантами, например . Определить число необходимых констант можно и иначе.
Работа внешних сил величина не отрицательная и зависит от нагрузок. От нагрузок
зависят и напряжения. В условиях монотонного роста нагрузки есть однозначная
зависимость между нагрузками и напряжениями, следовательно, можно обратить и
формально считать, что работа зависит от напряжений, а в системе главных
координат от главных напряжений. Они являются инвариантами тензора и могут быть
заменены любыми другими инвариантами, например 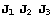 - линейным, квадратичным, и кубичным. То есть можем
считать - линейным, квадратичным, и кубичным. То есть можем
считать 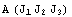 .
Разложим работу внешних сил в ряд Тейлора в окрестности нуля .
Разложим работу внешних сил в ряд Тейлора в окрестности нуля 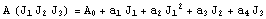 . В точке нуль . В точке нуль 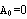 , нет напряжений - нет работы, , нет напряжений - нет работы, 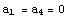 так как если это не так, то существует
возможность обратить работу в отрицательную величину, а это противоречит
определению работы. так как если это не так, то существует
возможность обратить работу в отрицательную величину, а это противоречит
определению работы.
Следовательно, остаются только квадратичные члены. Если
материал несжимаем при этих деформациях, то и первый инвариант нулевой. В итоге
для изотропного несжимаемого случая остается зависимость от одного
положительного скаляра, для определения которого и нужны эксперименты, которые
удобно провести на сжимаемом - растягиваемом стерженьке в условиях переменного
давления для моделирования различных напряженных состояний, так как
позволяют добавлять произвольную шаровую составляющую тензора к
девиатору, как это делали Карман и Бекер.
Девиатор можем рассматривать как вектор в девятимерном
пространстве, то есть, имеем векторное поле, определенное на деформируемом теле.
Напомним определение из математики: потенциальной функцией, или потенциалом
векторного поля σ называется скалярная функция F такая, что 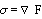 , где , где
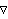 -
градиент. -
градиент.
Попробуем найти такую функцию для девиатора тензора, учитывая для
аналогии, что существует представление для простой переменной
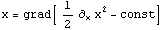

0
0
0
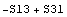

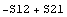
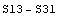

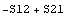
Из этих результатов видно, что если матрица или тензор
симметричные объекты, а в механике это обычно так, то потенциальная функция для
девиатора напряжений существует и его можно записать через след квадрата
девиатора
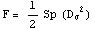 ,и эта
функция определяет пластический потенциал среды, а ее градиент направление
приращения пластической деформации. Тогда для пластических приращений деформации
справедливы соотношения ,и эта
функция определяет пластический потенциал среды, а ее градиент направление
приращения пластической деформации. Тогда для пластических приращений деформации
справедливы соотношения 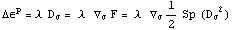 .
Другими словами поле девиаторов напряжений, а в силу пропорциональности и поле
приращений пластической деформации являются потенциальными полями. Потенциальная
функция обычно используется в дифференциальных операциях, поэтому в принципе
определена с точностью до константы, которую можно нагрузить дополнительным
смыслом. Уравнение F=const, или .
Другими словами поле девиаторов напряжений, а в силу пропорциональности и поле
приращений пластической деформации являются потенциальными полями. Потенциальная
функция обычно используется в дифференциальных операциях, поэтому в принципе
определена с точностью до константы, которую можно нагрузить дополнительным
смыслом. Уравнение F=const, или
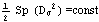 геометрически представляют собой поверхность, во всех точках которой потенциал
имеет одинаковую величину, такие поверхности обычно называются
эквипотенциальными поверхностями, или поверхностями уровня.
геометрически представляют собой поверхность, во всех точках которой потенциал
имеет одинаковую величину, такие поверхности обычно называются
эквипотенциальными поверхностями, или поверхностями уровня.
Для константы
обычно вводят специальное обозначение 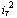 , где , где
 обычно называют
интенсивностью напряжений, как показано ниже, по механическому смыслу эта
величина равна касательным напряжениям в тонкостенной трубе в условиях кручения
или чистого сдвига. Математически это ситуация, когда тензор равен своему
девиатору. обычно называют
интенсивностью напряжений, как показано ниже, по механическому смыслу эта
величина равна касательным напряжениям в тонкостенной трубе в условиях кручения
или чистого сдвига. Математически это ситуация, когда тензор равен своему
девиатору.
Пластический потенциал обычно записывают в виде 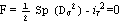 . Так
определенная потенциальная функция обычно называется пластическим потенциалом
Мизеса. Для среды всегда выполняется условие F≤0, при
отрицательных значениях потенциальной функции материал в исследуемой точке
находится в упругом состоянии, а при нулевом значении пластического потенциала в
пластическом. . Так
определенная потенциальная функция обычно называется пластическим потенциалом
Мизеса. Для среды всегда выполняется условие F≤0, при
отрицательных значениях потенциальной функции материал в исследуемой точке
находится в упругом состоянии, а при нулевом значении пластического потенциала в
пластическом.
Предельную интенсивность касательных напряжений, если она не
зависит от гидростатического давления, можно выразить через предел текучести в
одномерном растяжении или сжатии: 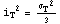 . В силу пропорциональности в векторном пространстве
приращений тоже будет поверхность уровня и эти две поверхности связаны через
коэффициент пропорциональности. Отсюда следует, что если известны значения
приращений для одной точки поверхности в пространстве приращений и согласованной
с ней точки в пространстве девиаторов напряжений или градиент квадрата
девиаторов, то можем вычислить коэффициент пропорциональности, который будет
справедлив для всех точек поверхностей уровня. Обычно известна информация по
одномерному растяжению. На ее основе обычно и вычисляют . В силу пропорциональности в векторном пространстве
приращений тоже будет поверхность уровня и эти две поверхности связаны через
коэффициент пропорциональности. Отсюда следует, что если известны значения
приращений для одной точки поверхности в пространстве приращений и согласованной
с ней точки в пространстве девиаторов напряжений или градиент квадрата
девиаторов, то можем вычислить коэффициент пропорциональности, который будет
справедлив для всех точек поверхностей уровня. Обычно известна информация по
одномерному растяжению. На ее основе обычно и вычисляют
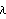
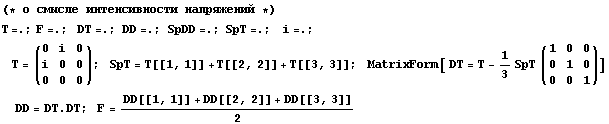
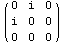 и и 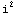

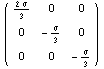 и и 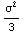
Таким образом, для одномерного случая справедливо соотношение,
из которого легко найти параметр пропорциональности.
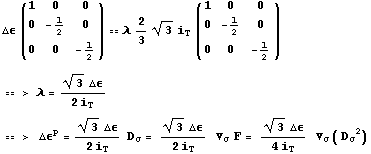
Здесь 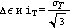 - приращения
пластической деформации и сдвиг для одномерного случая. - приращения
пластической деформации и сдвиг для одномерного случая.
Эти соотношения Рейса совпадают с соотношениями
использованными Хиллом, который приводит их в виде 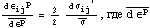 - приращение пластической деформации в одномерном случае, - приращение пластической деформации в одномерном случае, 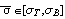 текущее значение растягивающего напряжения по
диаграмме текущее значение растягивающего напряжения по
диаграмме  для одномерного случая, зависящее от предыдущих
пластических деформаций, штрихом отмечается девиатор. для одномерного случая, зависящее от предыдущих
пластических деформаций, штрихом отмечается девиатор.
Запись приращения
пластической деформации через девиатор напряжений обычно связывают с
Сен-Венаном, а запись через градиент потенциальной функции с Мизесом. Если
определить эквивалент работы сил трения в теоретической механике - пластическую
работу как 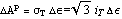 - получим, что эти соотношения можно
записать через пластическую работу и предельное напряжение. - получим, что эти соотношения можно
записать через пластическую работу и предельное напряжение. 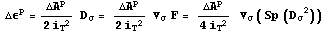
Все эти соотношения справедливы, если предельное напряжение
является константой, то есть в системе координат Мора горизонтальная линия.
Здравый смысл подсказывает, а эксперименты показывают, что это не так, и,
следовательно, предельная интенсивность касательных напряжений является функцией
не только от предыдущих деформаций, но и гидростатического давления. То есть,
как обобщали Мизес и Шлейхер, понятие напряжения эквивалентного растяжению.
Иначе, например, в условиях близких к всестороннему сжатию среда не могла бы
течь, и машиностроители не использовали бы сигма смятия, а физики были бы не
правы утверждая, что в условиях всестороннего сжатия хрупкие материалы
приобретают металлические свойства. Автору рассказывали, о результатах нагрузки
растяжением фарфоровых стерженьков при значительном всестороннем сжатии и эти
стерженьки вели себя как пластичные элементы, шейка образовывалась, и характер
разрушения был чисто пластическим.
Аналогично и в условиях близких к
всестороннему растяжению металлы не вели бы себя как хрупкие среды, и Биргер был
бы не прав, утверждая: "В этом случае оба критерия прогнозируют бесконечную
прочность, что не соответствует физическому смыслу понятия
прочности".
Возникает вопрос, почему в условиях всестороннего
сжатия-растяжения не наблюдается в экспериментах остаточной деформации, хотя
представленные кривые для поверхности текучести ограничены? Дело в том, что в
этом случае девиатор равен нулю, следовательно, и приращение пластической
деформации нулевое, но в случае небольшого возмущения, сразу появляется
пластическая деформация.
Проделаем мысленный эксперимент типа тех, что
физически осуществляли Карман и Бекер с мрамором. Пусть линейный образец,
доведенный до напряжения текучести, например в струбцине, помещается в сосуд, в
котором можно менять давление. Пусть схема предварительно приложенной нагрузки
такова, что при подаче давления обеспечивается возрастание гидростатического
давления в стержне. Как и ранее сделаем математическую модель
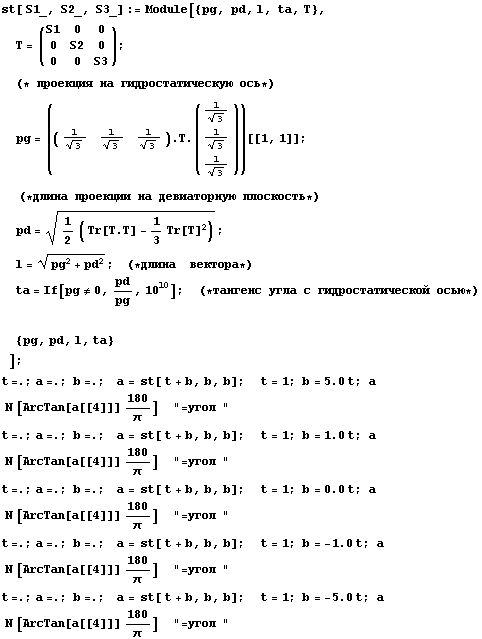
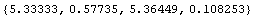 и и 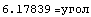
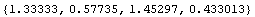 и и 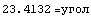
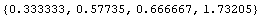 и и 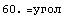
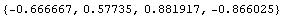 и и 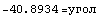
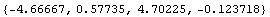 и и 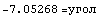
Из этих вычислений видим, что если принять независимость
интенсивности от девиатора (0.57735 в мысленном эксперименте), как это делается
в критерии Мизеса, то сигма текучести при одномерном растяжении будет
увеличиваться до 4...5 раз причем, независимо от того гидростатическое сжатие
или растяжение добавляется. Это противоречит интуиции и опытам многих
исследователей, для примера сошлемся на Хилла "текучесть имеет место при
напряжении σ-p , если к боковой поверхности растягиваемого образца приложено
гидростатическое давление умеренной величины p". Это высказывание относится к
опыту на растяжение образца из отожженной стали, с максимальным напряжением σ в
обычных условиях.
Следовательно, можно сделать вывод о том, что интенсивность
касательных напряжений достаточно сильно зависит от гидростатического давления,
значит, ее можно брать из кривых Мора полученных ранее при обработке
экспериментальной информации 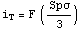 . .
Интуиция подсказывает, что поскольку геометрия
эксперимента не меняется, то приращение пластической деформации не будет
зависеть от гидростатического давления. Девиатор тензора напряжений по
определению не зависит от гидростатического давления. Приращение пластической
работы можно рассматривать как квадратичный функционал деформаций, зависящий и
от модуля упругости. Модуль упругости связан с межатомными
взаимодействиями, поэтому можно считать, что он не зависит от гидростатического
давления. Другими словами - приращение пластической работы геометрический
инвариант и не зависит от гидростатического давления.
Приведенное выражение для пластических деформаций 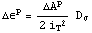 не слишком удобно для практических вычислений. Оно
практически состоит из двух частей - масштабного множителя и тензора, задающего
направление. Более естественно направление задавать в виде нормированного
тензора. Так как трехвалентный тензор можно рассматривать как вектор в
девятимерном пространстве, то его длину естественно определить обычным для
вектором способом как корень из скалярного квадрата вектора. В тензорном
обозначении как корень из двойного скалярного произведения тензоров. Проверим
эквивалентность этих величин для симметричных тензоров: не слишком удобно для практических вычислений. Оно
практически состоит из двух частей - масштабного множителя и тензора, задающего
направление. Более естественно направление задавать в виде нормированного
тензора. Так как трехвалентный тензор можно рассматривать как вектор в
девятимерном пространстве, то его длину естественно определить обычным для
вектором способом как корень из скалярного квадрата вектора. В тензорном
обозначении как корень из двойного скалярного произведения тензоров. Проверим
эквивалентность этих величин для симметричных тензоров:

В то же время, для несимметричного тензора эта эквивалентность
отсутствует, но в механике деформируемого тела тензоры обычно симметричные и это
не обременительное ограничение на нормировку.
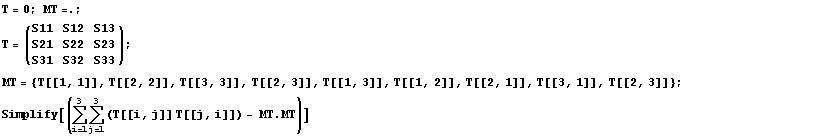
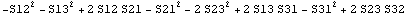
Как это принято будем обозначать двойное скалярное произведение
тензоров двумя точками, например,
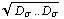 длина
девиатора напряжений. длина
девиатора напряжений.
Тогда приращение пластической деформации можно записать
в виде:
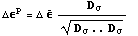 Здесь Здесь
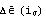 приращение
пластической деформации одномерного растяжения без давления. Приведение надо
осуществлять по линии текучести в координатах Мора. Величину приращения надо
определять из сигма-эпсилон кривой и приращения напряжений. приращение
пластической деформации одномерного растяжения без давления. Приведение надо
осуществлять по линии текучести в координатах Мора. Величину приращения надо
определять из сигма-эпсилон кривой и приращения напряжений.
Объединив приращение упругих деформаций с приращением
пластических деформаций, получим упругопластический аналог закона Гука в
приращениях, известный как уравнение Рейса:
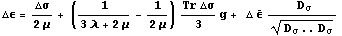
Из последнего соотношения видно, что связь приращений
деформаций и напряжений нелинейная, в отличие от закона Гука, который выражен в
двух первых слагаемых, здесь g- метрический тензор (единичная матрица, если
имеем матричное представление тензоров). В случае нулевого девиатора возникает
неопределенность и в практических вычислениях можно возмущать его через
использование машинного эпсилон и датчика случайных чисел, или принимать
приращение пластической деформации нулевым тензором. По крайней мере, в области
растяжений использование случайных малых возмущений выглядит более реалистично.
Да и в области сжатия для неоднородных материалов типа бетона это более
предпочтительно.
В каждой конкретной точке нагрузки, лежащей на поверхности
текучести, в которой и может быть приращение пластической деформации,
направление этого приращения должно лежать в девиаторной плоскости, проходящей
через эту точку. Иначе не будет обеспечена несжимаемость приращения
пластической деформации.
В изотропном материале поверхность текучести
представляет собой поверхность, образованную вращением образующей, описанной в
координатах Мора, вокруг гидростатической оси, следовательно, сечение этой
поверхности девиаторной плоскостью, проходящей через точку, будет окружностью.
Пластическая деформация связана с потерей внутренней упругой энергии и
переходе ее в тепловую энергию. В этом легко убедится, сгибая проволоку. Другими
словами энтропия системы возрастает, как и предписывает термодинамика. Из
равновесной термодинамики известен принцип Гиббса, по которому энтропия
изолированной системы достигает максимума на всех возможных состояниях системы с
заданным уровнем энергии. Другими словами приращение пластической деформации
должно обладать экстремальными свойствами, а из математики известно, что такими
свойствами обладает градиент поверхности.
То есть из физических соображений
логично принять, что пластическая деформация будет направлена по направлению
проекции градиента напряжений на девиаторную плоскость, то есть в направлении
 . Геометрический образ этого направления в главных осях
может быть образован пересечением девиаторной плоскости, проходящей через
заданную точку, и плоскости проходящей через заданную точку и гидростатическую
ось. . Геометрический образ этого направления в главных осях
может быть образован пересечением девиаторной плоскости, проходящей через
заданную точку, и плоскости проходящей через заданную точку и гидростатическую
ось.
Иногда эту идею описывают как экстремальный принцип с ограничением
равенством, обеспечивающим несжимаемость приращения пластической деформации.
Геометрический образ направления пластической деформации в
главных осях как вектора в девиаторной плоскости справедлив для несжимаемых
материалов. Но многие материалы в процессе деформации имеют и пластическое
изменение объема. Некоторые материалы могут разрыхляться, если есть
гидростатическое растяжение, и уплотняться, если есть гидростатическое сжатие.
Другие могут иметь одностороннее поведение, например можно принять, что
железобетон при гидростатическом растяжении расширяется за счет образования
микротрещин, но при гидростатическом сжатии пластического изменения объема не
происходит. Это логично учесть в виде гидростатической добавки к направлению
пластического деформирования. Геометрически это выразится в отклонении вектора
пластической деформации от девиаторной плоскости в ортогональном к этой
плоскости направлении на некоторый угол. Этот угол естественно назвать углом
расширения или сжатия и обычно его называют углом дилатации.
Рассмотрим напряжения в координатах Мора, при этом направление
пластической деформации в условиях несжимаемости всегда совпадает с вертикальным
направлением, а изменение объема с горизонтальным. Таким образом, в общем случае
пластической деформации это будет наклонный вектор. Отклонение от вертикали
определяется углом дилатации, то есть отношение приращения объемной деформации к
сдвиговой деформации определяет тангенс угла дилатации.
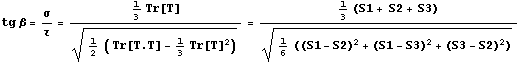
Направление гидростатической составляющей пластической
деформации естественно будет совпадать с единичной матрицей в матричном
представлении тензоров или с метрическим тензором в общем случае. При этом в
случае гидростатического растяжения будет происходить разрыхление, а при
гидростатическом сжатии уплотнение. Это хорошо для грунтов, пенобетона и других
подобных композитов, а для бетонов и скальных пород, определение угла отклонения
от девиаторной плоскости через константу уже не совсем подходит.
При трещинообразовании все нормально, но при сжатии
объемной пластической деформации не будет и угол надо определять как функцию
гидростатического давления. Условие 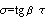 можно рассматривать как эквивалентное несжимаемости геометрическое
условие на направление пластической деформации. То есть направление определяется
пересечением конуса вокруг гидростатической оси с углом раскрытия можно рассматривать как эквивалентное несжимаемости геометрическое
условие на направление пластической деформации. То есть направление определяется
пересечением конуса вокруг гидростатической оси с углом раскрытия 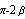 и плоскости проходящей через точку
нагрузки и гидростатическую ось. Геометрический образ естественно в системе
главных осей координат. и плоскости проходящей через точку
нагрузки и гидростатическую ось. Геометрический образ естественно в системе
главных осей координат.
Тензор приращения пластических деформаций логично нормировать.
Тогда можно записать аналог уравнений Рейса, обозначив за D девиатор
градиента, здесь как обычно D..D двойное скалярное произведение девиаторов или
двойная свертка:
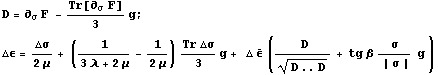
Для бетона угол дилатации надо еще умножить на функцию
включения (UnitStep в Mathematica), так как в условиях всестороннего сжатия его
можно считать пластически несжимаемым, так как микротрещин в этом случае не
образуется. Теория дело убедительное, но иногда полезно проверять на очевидных
частных случаях. Рассмотрим сжатие стержня из глины, как материала по разному
сопротивляющегося растяжению и сжатию, следовательно, в рамках линейной модели
разрушения можно считать, что поверхность разрушения описывается законом
Кулона 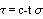 , где t- тангенс угла внутреннего трения , c- сцепление грунта. Изобразим график для
зависимости предельных сдвигов от гидростатического давления: , где t- тангенс угла внутреннего трения , c- сцепление грунта. Изобразим график для
зависимости предельных сдвигов от гидростатического давления:
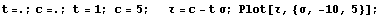
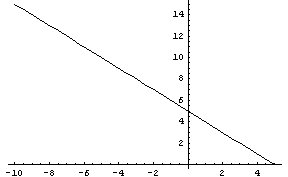
В многомерном случае для главных напряжений предельная
поверхность - конус, который обычно связывают с Друкером и Прагером.
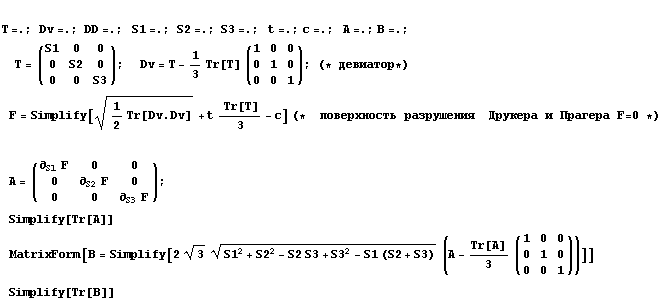
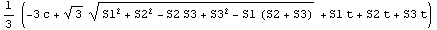
t
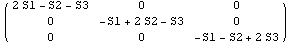
0
Это девиатор, определяющий направления пластической деформации
в общем случае для главных осей координат. В случае одномерного
растяжения:

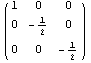
В этом случае направление пластической деформации совпадает с
направлением задаваемым девиатором напряжений и полностью согласуется со здравым
смыслом. Так как градиент является линейной операцией и не зависит от кривизны
поверхности, можем считать, что принцип определения направления пластического
деформирования через девиатор градиента от потенциальной функции, задаваемой
поверхностью текучести достаточно убедителен.
Теперь рассмотрим общий
случай. Для начала определимся с дифференцированием потенциальной функции по
симметричному тензору или квадратной симметричной матрице. В случае
несимметричной все достаточно очевидно, результатом дифференцирования по матрице
будет матрица, элементами которой будут производные функции по элементам
исходной матрицы, но в случае симметричной при дифференцировании по
недиагональным компонентам возникают проблемы из-за того, что в силу симметрии
эти элементы входят дважды. Поэтому сначала определим дифференцирование для
несимметричной матрицы, потом все симметризуем и покажем, что существует правило
для прямого определения производной по симметричной матрице в общем виде:

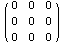
Нулевой результат говорит о тождестве этих операций. Сравним
теперь случай определения направлений пластической деформации через девиатор
напряжений и через производные от поверхности, задаваемой конусом
Друкера-Прагера в случае несжимаемости пластических деформаций.

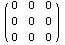
Попробуем еще усилить этот результат и проверим для
произвольных полиномиальных функций от гидростатического давления.

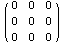
Чертовы штучки. Учитывая полученный результат, можем сделать
однозначный вывод - девиатор тензора напряжений обладает экстремальным
свойством, то есть направление им определяемое является направлением проекции
градиента любой поверхности образованной вращением вокруг гидростатической оси
на девиаторную плоскость.
Таким образом, не снижая общности, всегда можем
определять направление приращения пластической деформации для изотропных тел и
предположении о несжимаемости приращения пластических деформаций при известном
тензоре напряжений в точке, через его девиатор. Или как проекцию градиента
произвольной функции образованной вращением вокруг гидростатической оси на
гидростатическую плоскость, или как линию пересечения двух плоскостей проходящих
через точку при этом одна плоскость ортогональна гидростатической оси, а другая
проходит через нее. Определение направления пластической деформации через
девиатор тензора напряжений более предпочтительно, так как позволяет без
снижения точности и лишних гипотез использовать кусочно-гладкие аппроксимации
для поверхности текучести для определения направления текучести. В
вычислительной математике хорошо известно, что численное дифференцирование
вносит значительные ошибки по сравнению с другими операциями.
Можно выразить и приращения напряжений через приращения
деформаций. Для этого представим матрицу упругости изотропного материала через
коэффициенты Ляме в девятимерном пространстве напряжений, обратим ее и получим
матрицу податливостей.
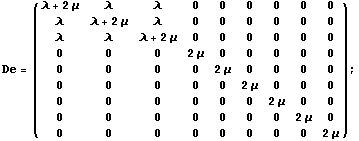
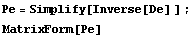
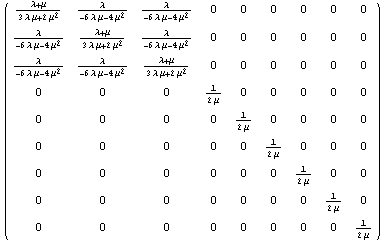
Следуя Зенкевичу, окаймим ее симметрично направляющим
тензором пластических деформаций, где
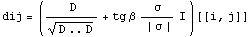 , где D -
девиатор напряжений, , где D -
девиатор напряжений, 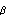 - угол
дилатации, - угол
дилатации, 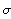 -
гидростатическое давление , I- единичная матрица, а
диагональный элемент окаймления обозначим -Et.
Физический смысл его рассмотрим позднее. -
гидростатическое давление , I- единичная матрица, а
диагональный элемент окаймления обозначим -Et.
Физический смысл его рассмотрим позднее.
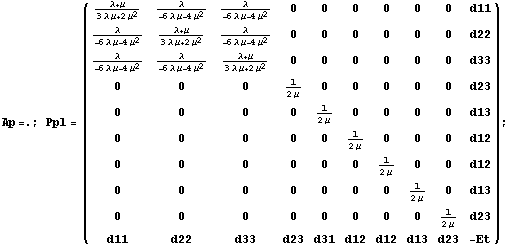
По правилу Крамера элементы обратной матрицы имеют
представление, в котором присутствует деление на определитель матрицы.
Далее обратим окаймленную матрицу податливости. Затем для упрощения
результатов умножим на числитель определителя и упростим:
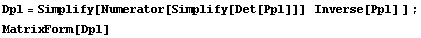
В силу независимости компонент тензора направлений приращения
пластической деформации от коэффициентов Ляме и их комбинаций, понятно, что
обращение можно осуществить при любом Et, в том числе и нулевом.
Покажем
это:
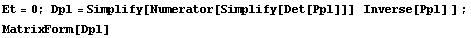
Для определения смысла Et рассмотрим одномерное растяжение и
пусть  напряжение, напряжение, 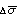 - приращение
напряжения, а - приращение
напряжения, а 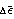 приращение
деформации и пусть материал находится в упругопластическом состоянии. Тогда
направление пластической деформации можно определить приращение
деформации и пусть материал находится в упругопластическом состоянии. Тогда
направление пластической деформации можно определить
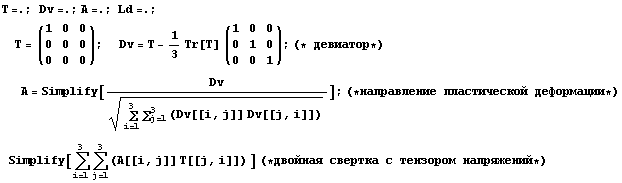
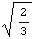
Приращение напряжения будет только по первой координате и,
рассматривая последнюю строку матрицы податливости, можем записать 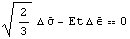 . Теперь можем определить . Теперь можем определить 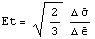 , где , где 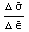 обычно называется касательным, или тангенциальным модулем на
диаграмме растяжения-сжатия материала. обычно называется касательным, или тангенциальным модулем на
диаграмме растяжения-сжатия материала.
Таким образом, соотношениям теории пластичности можно придать
матричный вид, похожий на закон Гука 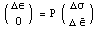 , по существу уравнения Прандтля-Рейса, или обратные
соотношения , по существу уравнения Прандтля-Рейса, или обратные
соотношения 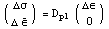 ,
где P матрица упруго пластической податливости, а ,
где P матрица упруго пластической податливости, а 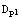 упругопластическая матрица. Все эти соотношения для приращений или
инкрементальные, при желании им можно придать дифференциальную форму или поделив
на
упругопластическая матрица. Все эти соотношения для приращений или
инкрементальные, при желании им можно придать дифференциальную форму или поделив
на 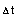 и осуществив
предельный переход придать вид соотношений между скоростями. и осуществив
предельный переход придать вид соотношений между скоростями.
Если материал подобно грунтам может уплотняться или
разрыхляться, то это можно учесть добавив к пластической деформации
гидростатическую добавку, подобно тому, как это делается в законе Гука в теории
упругости.
Как упрощенный вариант можно просто добавить квадратичную добавку,
которая, например, скорректирует конус Друкера-Прагера так, чтобы в области
сжатия отклонение образующей в координатах Мора осуществлялось вверх, а в
области растяжения проседало вниз. При этом конус Друкера-Прагера будет
образован вращением кривой второго порядка относительно гидростатической оси. В
литературе встречается информация, что при взрыве упаковка грунта может
достигать 30%. Таким подходом к изменению поверхности текучести конечно не
учитывается реальное изменение плотности малого объема, но учитывается
возрастание или снижение его накапливать упругую энергию, так как упругая
энергия может рассматриваться как квадратичная форма от тензора упругих
напряжений. В случае уплотнения или разрыхления материала естественно изменяется
и модуль упругости и коэффициент Пуассона. Учесть эти изменения можно по
технологии описанной в статье об осреднении.
Не представляет особого труда сделать поверхности текучести и
разрушения и функцией температуры и при необходимости других физических
параметров.
Вопросы постановки и решения упругопластических, то есть
нелинейных задач требуют отдельного рассмотрения, что и будет сделано в одной из
следующих статей.
- Работнов Ю.Н. Механика деформируемого твердого тела: - М.: Наука 1988.
- Филоненко-Бородич М.М.
Механические теории прочности. М. 1961
- Хилл Р. Математическая теория пластичности. М.1956
- Качанов Л.М. Основы теории пластичности. М.Наука. 1969
- Биргер И.А.,Мавлютов Р.Р. Сопротивление материалов. М.:Наука. 1986
- Анурьев В.И. Справочник конструктора-машиностроителя. Т 1. 2003
- Коллинз Дж. Повреждение материалов в конструкциях. Анализ, предсказание, предотвращение. М.Мир.1984
В начало |

