Для чего созданы
компьютеры?
Для облегчения счета, для хранения информации,
для переработки информации, для слежения за
физическими процессами в реальном режиме
времени, для подготовки текста к печати, для
удобного управления системой с большим
объемом определяющих ее параметров, для
Интернета и т.д.
Приведенный ответ верен, но от части и
даже от малой части. Заметим, что все
вышеперечисленное носит в известной степени
технический характер. Конечно, важно иметь
средство для быстрого и точного счета; конечно,
важно иметь средство для надежного удобного и
объемного хранения информации; конечно важно
иметь возможность секунда в секунду влиять на
быстроменяющийся объект и безусловно важно
печатать и исправлять тексты, предназначенные
для опубликования в печати. Что касается
Интернета, то, возможно, этот вопрос связан с
новым уровнем цивилизации.
Но вот еще один ответ на поставленный
вопрос. Компьютеры созданы математиками для
решения их тонких и хитроумных задач.
По значимости для "народного
хозяйства" перечисленные выше достоинства
компьютеров вряд ли можно преувеличить. Один
Интернет чего стоит. Но все же, все же.
Не так уж хитро придумать способ
быстрого счета (а затем использовать
быстродействие электронных приборов. Не так уж в
принципе хитро разложить по многочисленным
"полочкам" различные исходные данные (пусть
и очень многочисленные). Имея базу данных, можно
предложить способ преобразовать нужным образом
хранимую информацию или использовать ее для
решения хозяйственных задач. (Хороший пример -
автоматическое начисление заработной платы на
больших производствах). Печатание и
редактирование текста всегда считалось
квалифицированной, но выдающейся деятельностью.
Слежение за ракетой в реальном режиме времени
требует, конечно, знания законов механики,
теории дифференциальных уравнений, а также
теории оптимального управления. Главное
преимущество компьютера здесь - в
быстродействии, т.е. в техническом аспекте.
Интернет хотя и невозможно переоценить, все-таки
представляет из себя телефон с базой данных и
некоторым (уже значительно развитым) способом
поиска, хранения и обработки информации.
Другое дело те хитроумные и тонкие
математические задачи, которые интересуют
математиков.
Примеры
1. Задача Штейнера
2. Шахматы
3,4... Задачи распознавания
образов, криптографии, построения моделей
различных процессов
1. Задача Штейнера
На плоскости дано n точек.
Требуется соединить их так,чтобы длина
связывающей линии была бы наименьшей из всех
возможных. Здесь "связать" означает
включить данное множество точек в связное
множество, состоящее из кусков простых кривых.
Задача важна с практической точки зрения. Ее
решение требуется при планировании сети
железных дорог, связывающей данные точки-города,
при планировании трубопроводов, сети телефонных
кабелей и т.п. Задача достаточно трудная. Даже в
случае четырех точек, ннаходящихся в вершинах
некоторого квадрата. Оказывается решение задачи
в этом случае имеет следующий вид:
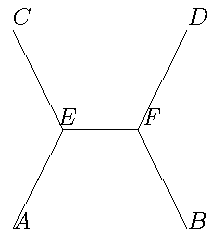
Здесь A, B, C, D - заданные точки, E,
F - точки разветвления (оказывается,
оптимальное решение задачи требует наличия
таких точек). При этом каждый из трех углов с
вершинами в точках E, F равен 120 градусам.
Суммарная длина всех отрезков на чертеже равна 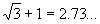 . Между прочим
сумма двух диагоналей нашего квадрата равна . Между прочим
сумма двух диагоналей нашего квадрата равна 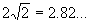 . Таким образом,
суммарная длина отрезков на рисунке меньше, чем
длина двух диагоналей квадрата, и соединение
точек A, B, C, D двумя диагоналями не является
наилучшим соединением, хотя, на первый взгляд
является таковым. . Таким образом,
суммарная длина отрезков на рисунке меньше, чем
длина двух диагоналей квадрата, и соединение
точек A, B, C, D двумя диагоналями не является
наилучшим соединением, хотя, на первый взгляд
является таковым.
Можно себе представить насколько
сложным и причудливым будет решение задачи
Штейнера в общем случае.
2. Шахматы
Задача состоит в том, чтобы в каждой
шахматной позиции найти наилучший (по крайней
мере, хороший) ход. Разумеется, компьютеру
придется рассматривать возможные позиции,
возникающие после тех или иных анализируемых
ходов. Если бы можно было перебрать все возможные
варианты, то задача стала бы чисто технической и
не интересной с математической точки зрения. В
действительности перебрать все варианты
невозможно - компьютеру просто не хватает
мощности. При этом задача становится много
интересней, поскольку требует надежной
(числовой) оценки позиции. Из допустимых
вариантов машина выбирает ход, который по
разработанному критерию дает наилучшую оценку.
Отбор допустимых вариантов и выбор
хорошего критерия и является той хитрой
математической задачей, при решении которой
раскрываются самые сильные стороны компьютера.
3,4,... Задачи распознавания
образов, криптографии, построения моделей
различных процессов
Чтобы компьютер работал над задачей,
нужны алгоритм и программа. Что касается
алгоритма, то это чисто математический вопрос.
Программа, осуществляющая алгоритм, пишется на
некотором машинном языке (Бэйсик, Паскаль, Си,
Ассемблер, Фортран и др.), один язык от другого
отличается степенью удобства излагать алгоритмы
в командах этого языка.

Система Mathematica,
созданная лет десять тому назад в своих
последних версиях (Mathematica 3.0, Mathematica 4.0) имеет
чрезвычайно широкий набор средств, переводящих
сложные математические алгоритмы в программы.
Все так называемые элементарные функции и
огромное количество неэлементарных.
Алгебраические и логические операции. По сути
дела все алгоритмы, содержащиеся в курсе высшей
математики ведущего технического вуза заложены
в память компьютерной системы Mathematica. Это значит,
между прочим, что большинство упражнений из
курса высшей математики может быть решено с
помощью всего лишь одной команды. Действительно,
все упражнения из линейной алгебры (включая
такие нетривиальные вещи как приведение
квадратичных форм к каноническому виду,
приведение линейного оператора к жордановой
форме). Все упражнения из анализа, теории
дифференциальных уравнений (как
обыкновенных,так и в частных произвожных). С
помощью системы Mathematica можно вычислять интегралы
(определенные и неопределенные), решать
дифференциальные уравнения (численно и
аналитически). Mathematica знает об интегралах и
дифференциальных уравнениях больше, чем любой
толстый справочник. Кроме того, Mathematica не только
дает окончательный ответ, но может описать
промежуточные вычисления (например, разложение
правильной рациональной функции в сумму
элементарных дробей, что требуется при
интегрировании рациональных функций).
Mathematica имеет мощный графический пакет.
С ее помощью можно строить графики очень сложных
функций одного и двух переменных. При этом
получаются часто восхитительно красивые
картинки.
Сверх всего этого Mathematica решает задачи,
известные только специалистам. Например, задачу
Вороного. В этой задаче дано N точек на
плоскости
P1, P2, ..., Pn и
требуется разбить плоскость на многоугольники
S1, S2, ..., Sn так,
чтобы
Sk=( X | r (X,
Sk)< r (X, Sl),
l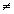 k ). k ).
По-прежнему задача решается одним нажатием
клавиши.
В современной математической науке
большую роль играет так называемая дзета
функция Римана z(z). По определению
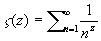 . .
Существует гипотеза о нулях этой
функции комплексного переменного z. Верно
ли, что все нули этой функции, т.е. такие комплексные
числа z, что
z(z)=0, обладают свойством Rez(z)=1/2? Этой гипотезе уже много лет. Она
до сих пор не доказана и не опровергнута.
Гипотеза Римана принадлежит к классу
знаменитых математических проблем, решение
которых является вожделенной целью
математической науки - таких как проблемы
Гильберта, проблема Бернсайда, гипотеза Ферма,
проблема Пуанкаре, гипотеза континуума,
классификация простых конечных групп и
др. Некоторые из перечисленных задач к настоящему
времени уже решены, некоторые еще нет. Среди
последних - гипотеза Римана. Mathematica, конечно не
может решить проблему Римана, но она может одним
нажатием клавиши установить те области на
плоскости комплексного переменного, где |z(z)|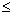 e для любого e e для любого e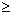 0. 0.
Упомянем еще о некоторых
преимуществах системы Mathematica.
Наберем на дисплее 1000! и нажмем клавишу Enter. Сразу
же на экране появятся цифры. Их будет много, они
займут весь экран. Придется прокрутить экран,
прежде чем достигнем конца этой
последовательности цифр. Таков результат
вычисления тысяча факториал. Очень впечатляет.
Можно взять и 10000!. Mathematica может работать с числами
сколь угодно большими. (Заметим, что во многих
компьютерных языках для действия с большими
числами нужно предпринять дополнительные меры).
Mathematica содержит удобный способ работы
с векторами и тензорами.
Огромное преимущество системы Mathematica
состоит в том, что множество ее операторов и
способы записи алгоритмов просты и естественны.
Как правило, здесь не надо особенным
образом заранее объявлять тип переменных, не
надо специально распределять память для
хранения той или иной информации. По простоте
работы Mathematica превосходит Basic. Это происходит за
счет укрупнения команд, которое делает написание
программ в Mathematica более коротким и удобным. Это
значит, что научиться работать в системе Mathematica
довольно просто.
И, наконец, последнее преимущество
системы Mathmatica, делающее ее бесспорным лидером
среди других систем высокого уровня таких как
Maple, Mathcad, Mathlab и др. Система Mathematica уже очень широко
распространена в мире, ею захвачены огромные
области применения в научных и инженерных
исследованиях а также в системе образования.
Действительно, существует и процветает большая
компания Wolfram Research. Большая группа весьма
искусных математиков этой компании постоянно
усовершенствует систему Mathematica (версии 2.0, 3.0 и
последняя 4.0). Ежемесячно выпускается журнал с
обсуждением актуальных проблем, существует сайт
в Интернете, ведется активная работа с
пользователями. На всемирных математических
конгрессах (раз в четыре года) Wolfram Research имеет
свой стенд, а математики из этой компании читают
лекции и проводят семинары. В некоторых странах
(например в США) вузовская система образования
тесно связана с системой Mathematica. Написано
несколько книг учебного характера с
использованием системы Mathematica (см. ,например,
А.Грей "Трубки", Наука,перевод с английского,
1997).
Почему будущее за системой Mathematica?
Потому, что она уже широко внедрена в
практику.
Потому, что она широко рекламирована.
Потому что она хорошо приспособлена к
исследовательским и учебным задачам.
Потому что она опирается на
постоянную весьма квалифицированную работу
группы математиков Wolfram Research.
Положение вещей здесь можно сравнить с
недавней ситуацией на компьютерном рынке.
Конкурировали многочисленные модели
компьютеров, а победил (и уже по-видимому
окончательно) Билл Гейтс. С дистанции сошли вовсе
не плохие компьютеры - они не смогли
конкурировать с победителем, который захватил и
освоил огромный рынок. Теперь даже очень
хорошему новому компьютеру трудно будет найти
место под солнцем в условиях, когда основной
потребитель компьютеров связан системой Windows,
набором запасных блоков и т.д.

Mathematica в образовании в скорм времени
должна начать играть очень важную роль. Уже
упоминалось о том обстоятельстве, что буквально
все упражнения в курсе высшей математики
могут быть решены компьютерной системой
нажатием одной клавиши. Это обстоятельство имеет
очень большое положительное значение. При этом,
однако, возможна возникновение следующей
методической дискуссии по поводу широкой
применимости системы Mathematica в образовании.
Та сторона в дискуссии, которая против
широкого применения системы Mathematica может
опираться на такие доводы:
"Применение компьютерной системы
Mathematica нецелесообразно, так как вместо глубокого
изучения предмета дело ограничивается лишь
нажатием кнопок."
"Применение системы Mathematica
затруднительно потому, что в настоящее время
программы пакета Mathematica дороги".
"Система Mathematica предназначена для
научных и исследовательских работ, а для
обучения студентов и школьников нужны другие,
специализированные и более дешевые
программы".
По нашему мнению эти доводы
несостоятельны. Вот наши контраргументы.
Никто не собирается заменять все
преподавание вычислительной работой на
компьютере. При сохранении традиционной формы
преподавания можно часть времени уделить
компьютерной стороне дела. Это будет иметь
большое значение как наглядное, так и
контрольное (и как результат - качественное).
Известно, что многие вопросы математики трудно
излагаются на лекциях ввиду большой
вычислительной работы, необходимой для
иллюстрации материала. Mathematica здесь может сильно
помочь.
Следует различать компьютерный
практикум и полное внедрение в программу
изучения курса математики компьютерного
сопровождения этого курса. Мы
придерживаемся той
точки зрения, что такое внедрение произошло как
можно раньше. Для этого, правда , потребуется
решение некоторых непростых чисто методических вопросов. В
частности, следствием такой точки зрения
является издание учебников нового поколения,
учитывающих систематическое применение пакета
Mathematica.
Что касается дороговизны пакета
Mathematica, то это дело относительное. Известно, что
компьютерные продукты постоянно дешевеют. Кроме
того, говоря о будущем и о таких важных вещах как
образование, не стоит экономить на малом. Еще
недавно экономили на компьютерах, заменяли их на
более дешевые. В конечном итоге оказалось, что
нужно ориентироваться на современные
стандартные и высокого уровня компьютеры.
Нужны ли специальные компьютерные
программы для обучения студентов и школьников?
По нашему мнению не нужны. Во-первых, система
Mathematica имеет одной из своих главных целей именно
обучение (студентов, школьников и др.) Во-вторых,
создание специальной (глобальной) системы для
образования требует исключительно больших
интеллектуальны усилий большого и
квалифицированного коллектива. Это
действительно будет очень дорого. Дорого
создать, дорого разрекламировать, дорого
внедрить. В отношении системы Mathematica все это уже
сделано, и сделано на очень высоком (выдающемся)
уровне. Тот факт, что система Mathematica содержит
больше, чем нужно для обучения не является
аргументом против широкого применения
системы Mathematica. Ведь современные компьютеры
часто и плодотворно используются для
сравнительно узких целей. При этом не возникает
вопроса о том, чтобы заменить их на более
маломощные и более дешевые.
Развивая мысль о
широком внедрении системы Mathematica в образовании,
отметим следующие первоочередные задачи в этом
направлении.
Следует издать полноценные
руководства по компьютерной системе Mathematica. В
настоящее время их почти нет на русском языке.
(Среди вышедших из печати кратких руководств
отметим книгу Капустиной Т.В. "Компьютерная
система Mathematica для пользователей",
издательство СОЛОН, Москва, 1999.
Следует издать учебники нового типа с
систематическим применением компьютерной
системы Mathematica. По крайней мере, существующие
традиционные учебники должны быть переизданы в
варианте, где все изложение сопровождается
иллюстрациями из системы Mathematica. Тем более, что
такая тенденция уже явно прослеживается в
западных странах.

Книга содержит
достаточно подробное описание системы Mathematica.
Настолько подробное, что после некоторого
вникание в суть дела читатель может начать
самостоятельно писать собственные программы.
Mathematica имеет огромное количество команд и
операторов. Все их запомнить невозможно. Важно
знать (немногочисленные) главные команды.
Существенное значение имеют вопросы интерфейса,
к которым надо привыкнуть. Всем этим
обстоятельствам в книге уделено должное
внимание.
Среди основных понятий системы Mathematica
особое внимание уделено понятию "шаблона"
(pattern). Оно имеет принципиально важное значение.
Являясь по своему существу понятием
математической науки, оно тем не менее не
употребляется в теоретической математике.
Возможно, в будущем под влиянием системы Mathematica
оно станем стандартным общепринятым
математическим понятием.
Вторая часть книги посвящена
алгоритмам и программам, решающим ряд интересных
и нетривиальных математических задач. Вот их
перечень.
Задача об оптимальной стратегии
торговли на аукционе. Ценообразование в условиях
конкуренции.
Сечение четырехмерного куба
гиперплоскостью.
Проверка гипотезы
Гольдбаха для
большого отрезка натурального ряда.
Построение и анализ d-диаграмм.
Мероморфные узлы.
Вероятности в преферансе.
Игра Ним.
Разложение тензорных произведений
представлений полупростых алгебр Ли.
Хордовые диаграммы и соответствующие
им инвариантные тензоры.
Книга планируется к изданию в 2000 году в
издательстве "Финансы и статистика".

|

