|
Чтобы определить матрицу нужно:
- ввести с клавиатуры имя матрицы и знак
присваивания (для ввода знака присваивания нужно
нажать на клавиатуре комбинацию клавиш <Shift>+<:>
или щелкнуть по кнопке<:=> панели Evaluation);
- щелкнуть по кнопке Vector or Matrix Toolbar в
панели математических инструментов, чтобы
открыть панель матричных операций Matrix);
- открыть щелчком по кнопке Matrix or Vector
окно диалога определения размерности матрицы и
ввести размерность матрицы: число строк (Rows),
число столбцов (Columns);
- закрыть окно диалога, щелкнув по кнопке Ok.
В рабочем документе, справа от знака
присваивания, открывается поле ввода матрицы с
помеченными позициями для ввода элементов.
Для того, чтобы ввести элемент матрицы,
установите курсор в помеченной позиции и введите
с клавиатуры число или выражение.

Номер первой строки (столбца) матрицы или
первой компоненты вектора, хранится в Mathcad в
переменной ORIGIN.
По умолчанию в Mathcad координаты векторов, столбцы
и строки матрицы нумеруются начиная с 0 (ORIGIN:=0).
Поскольку в математической записи чаще
используется нумерация с 1, удобно перед
началом работы с матрицами определять
значение переменной ORIGIN равным 1,
выполнять команду
ORIGIN:=1.

Панель векторных и матричных операций
открывается щелчком по кнопке Vector and Matrix
Toolbar в панели математических
инструментов.
За кнопками панели закреплены следующие
функции:
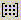 —
определение размеров матрицы; —
определение размеров матрицы;
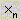 — ввод нижнего
индекса; — ввод нижнего
индекса;
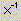 —
вычисление обратной матрицы; —
вычисление обратной матрицы;
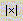 —
вычисление определителя матрицы: |A|=det A;
вычисление длины вектора |x|; —
вычисление определителя матрицы: |A|=det A;
вычисление длины вектора |x|;
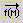 —
поэлементные операции с матрицами: —
поэлементные операции с матрицами:
если A={aij }, B={bij }, то 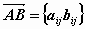 ; ;
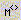 —
определение столбца матрицы: —
определение столбца матрицы: 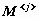 — j -й столбец матрицы M; — j -й столбец матрицы M;
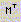 —
транспонирование матрицы: M={mij }, M T
={mji }; —
транспонирование матрицы: M={mij }, M T
={mji };
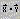 —
вычисление скалярного произведения векторов: —
вычисление скалярного произведения векторов: 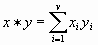 ; ;
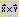 —
вычисление векторного произведения векторов: —
вычисление векторного произведения векторов:
a x b = (a2 b3 -a3 b2 , a3
b1 -a1 b3 , a1 b2 -a2 b1
);
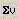 —
вычисление суммы компонент вектора: —
вычисление суммы компонент вектора: 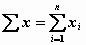 ; ;
 —
определение диапазона изменения переменной; —
определение диапазона изменения переменной;
 —
визуализация цифровой информации, сохраненной в
матрице. —
визуализация цифровой информации, сохраненной в
матрице.
Для того чтобы выполнить какую-либо операцию с
помощью панели инструментов, нужно выделить
матрицу и щелкнуть в панели по кнопке операции,
либо щелкнуть по кнопке в панели и ввести в
помеченной позиции имя матрицы.

Меню символьных операций с матрицами (пункт
Matrix меню Symbolics) содержит три
функции:
- транспонирование (Transpose),
- обращение матрицы (Invert),
- вычисление определителя матрицы (Determinant).
Если требуется произвести какую-либо операцию
через пункт Matrix меню Symbolics,
нужно выделить матрицу и щелкнуть в меню по
строке нужной операции.

Функции, предназначенные для решения задач
линейной алгебры, можно разделить на три группы.
- Функции определения матриц и операций с блоками
матриц.
|
подробная информация
о функциях,
пример |
- Функции отыскания различных числовых
характеристик матриц.
|
подробная информация
о функциях,
пример |
- Функции, реализующие численные алгоритмы
решения задач линейной алгебры.
|
подробная информация
о функциях,
пример |
- matrix(m, n, f) — создает и заполняет матрицу
размерности m x n, элемент
которой, расположенный в i -й строке, j -м
столбце, равен значению f(i, j) функции f(x, y);
- diag(v) — создает диагональную матрица,
элементы главной диагонали которой хранятся в
векторе v;
- identity(n) — создает единичную матрицу порядка
n;
- augment(A, B) — формирует матрицу, в первых с т о л
б ц а х которой содержится матрица A, а в
последних — матрица B (матрицы A и B
имеют одинаковое число строк);
- stack(A, B) — формирует матрицу, в первых с т р о к
а х которой содержится матрица A, а в
последних — матрица B (матрицы A и B
имеют одинаковое число столбцов);
- submatrix(A, ir, jr, ic, jc) — формирует матрицу,
которая является блоком матрицы A,
расположенным в строках с ir по jr и в
столбцах с ic по jc, ir <= jr, ic <= jc.
Пример 1. Примеры исполнения
функций matrix, diag, identity, augment, stack, submatrix
- last(v) — вычисление номера последнего
элемента вектора v;
- lenght(v) — вычисление количества элементов v вектора;
- rows(A) — вычисление числа строк в матрице A;
- cols(A) — вычисление числа столбцов в матрице A;
- max(A) — вычисление наибольшего элемента в
матрицы A;
- tr(A) — вычисление следа квадратной матрицы A
( след матрицы равен сумме ее диагональных
элементов);
- rank(A) — вычисление ранга матрицы A;
- norm1(A), norm2(A), norme(A), normi(A) — вычисление норм
квадратной матрицы A.
Пример 2. Примеры исполнения
функций last, length, rows, cols, max, min, tr, rank, norm1, norm2, norm3
- rref(A) — приведение матрицы к ступенчатому
виду с единичным базисным минором (выполняются
элементарные операции со строками матрицы);
- eigenvals(A) — вычисление собственных значений
квадратной матрицы А ;
- eigenvecs(A) — вычисление собственных векторов
квадратной матрицы А; значением функции
является матрица, столбцы которой есть
собственные векторы матрицы А; порядок
следования векторов отвечает порядку следования
собственных значений, вычисленных функцией eigenvals(A);
- eigenvec(A, l) — вычисление собственного вектора
матрицы А, отвечающего собственному значению
l;
- lsolve(A, b) — решение системы линейных
алгебраических уравнений Ax=b.
Пример 3. Примеры исполнения
функций eigenvals, eigenvecs, eigenvec, lsolve

|

