  Каждый
график на чертеже зависит от дискретной
переменной. Эта дискретная переменная должна
появиться и в выражении для абсцисс, и в
выражении для ординат. Mathcad отображает одну точку
для каждого значения дискретной переменной.
Построение декартова графика
Самый простой график показывает значения
функции на интервале. Первый график на Рисунке 2
ниже иллюстрирует этот тип графика. Для его
создания сделайте следующее:
- Определите дискретную переменную x, которая
принимает значения в желаемом диапазоне
значений аргумента.
- Напечатайте выражение, график которого нужно
получить, в среднем поле на оси ординат и
напечатайте x в среднем поле на оси абсцисс.
- Нажмите [F9], чтобы увидеть график.
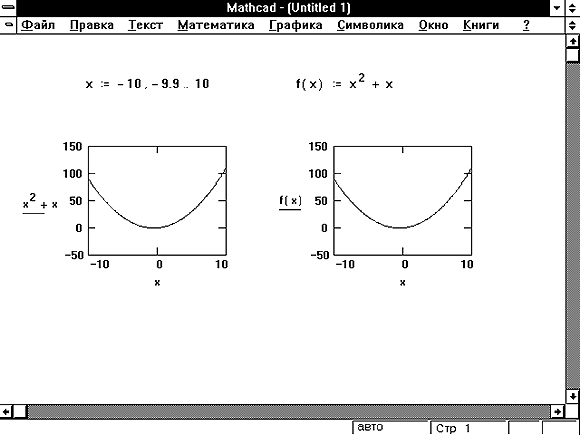
Рисунок 2:Построение графика выражения,
зависящего от дискретной переменной.
Можно также определить функцию f(x) и
поместить её в среднее пустое поле оси ординат.
Это особенно полезно для функций, представляемых
громоздким выражением. Второй чертёж на Рисунке 2
показывает тот же самый график, что и первый, за
исключением обозначения функции.
Можно перемещать, вырезать, копировать и
вставлять график, точно так же, как выражение.
Чтобы удалить график из рабочего документа:
- Нажмите и держите кнопку мыши где-нибудь вне
графика.
- При нажатой кнопке переместите курсор мыши,
чтобы включить графическую область в пунктирный
выделяющий прямоугольник.
- Нажмите [Ctrl]X, чтобы удалить график.
Можно также выбрать Вырезать из меню Правка.
Чтобы переместить график, следуйте приведенным
выше инструкциям для его удаления. Затем
щёлкните мышью там, где нужно вставить график и
выберите Вставить из меню Правка. Другие
способы перемещения графиков совпадают со
способами перемещения формул.
Использование функций для графиков в полярных
координатах.
Творчески используя инструментальные
средства, представленные в этой главе, можно
построить разнообразные замкнутые кривые.
Пример на Рисунке 3 иллюстрирует, как
преобразовать полярные координаты в
прямоугольные. Эта методика позволит создать
графики в полярных координатах или даже пути в
комплексной плоскости.
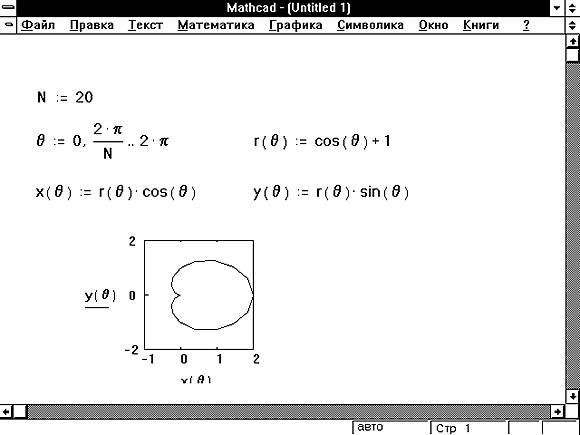
Рисунок 3: Две функции, вычисленные независимо.
На Рисунке 3 приводится уравнение кардиоиды в
полярных координатах, задаваемое в виде r(q).
Уравнения для x(q) и y(q) — обычное
преобразование от полярных координат к
прямоугольным. Описание встроенных в Mathcad
возможностей рисования в полярных координатах
находятся в Главе “Полярные
графики”.
  
|

