  Интерполяция
использует значения некоторой функции, заданные
в ряде точек, чтобы предсказать значения функции
между ними. В Mathcad можно или соединять точки
данных прямыми линиями (линейная интерполяция)
или соединять их отрезками кубического полинома
(кубическая сплайн-интерполяция).
В отличие от функций регрессии, обсуждаемых в
следующем разделе, функции интерполяции
определяют кривую, точно проходящую через
заданные точки. Из-за этого результат очень
чувствителен к ошибкам данных. Если данные
зашумлены, следует рассмотреть возможность
использования регрессии вместо интерполяции.
Линейное предсказание заключается в
использовании существующих значений данных,
чтобы предсказать значения за их пределами. В
Mathcad есть функция, которая позволяет
предсказывать будущие значения данных на основе
уже имеющихся данных.
Всякий раз, когда массивы используются в любой
из функций, описанных в этом разделе, убедитесь,
что каждый элемент массива содержит
определённое значение, так как Mathcad присваивает
значение 0 любым элементам, которые явно не
определены.
Линейная интерполяция
При линейной интерполяции Mathcad соединяет
существующие точки данных прямыми линиями. Это
выполняется функцией linterp, описанной ниже.
| linterp (vx, vy,
x) |
Использует векторы данных vx
и vy, чтобы возвратить линейно
интерполируемое значение y, соответствующее
третьему аргументу x. Аргументы vx и vy
должны быть векторами одинаковой длины. Вектор vx
должен содержать вещественные значения,
расположенные в порядке возрастания. |
Эта функция соединяет точки данных
отрезками прямых, создавая таким образом
ломаную. Интерполируемое значение для
конкретного x есть ордината y
соответствующей точки ломаной.
Для значений x, расположенных перед
первой точкой в vx, Mathcad продолжает ломаную
прямой линией, проходящей через первые две точки
данных. Для значений x, расположенных за
последней точкой в vx, Mathcad продолжает ломаную
прямой линией, проходящей через последние две
точки данных.
Для получения наилучших результатов значение x
должно находиться между самым большим и самым
маленьким значениями в векторе vx —
маловероятно, что будут полезны значения,
вычисленные для x вне этого диапазона.
Функция linterp предназначена для интерполяции,
а не экстрaполяции. Рисунок 5 показывает
некоторые примеры линейной интерполяции.
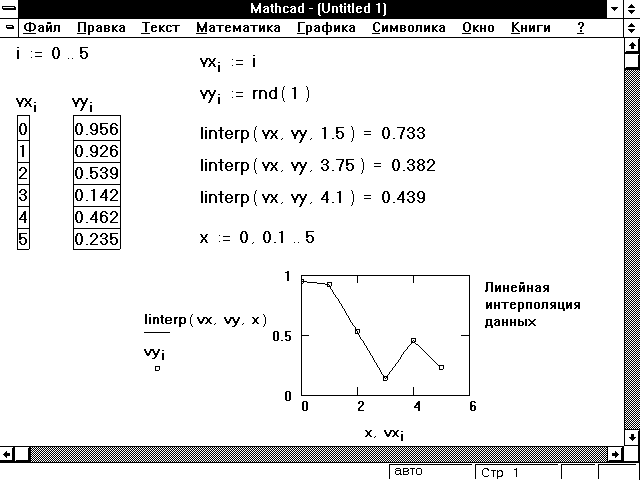
Рисунок 5: Примеры линейной интерполяции.
Кубическая сплайн-интерполяция
Кубическая сплайн-интерполяция позволяет
провести кривую через набор точек таким образом,
что первые и вторые производные кривой
непрерывны в каждой точке. Эта кривая образуется
путем создания ряда кубических полиномов,
проходящих через наборы из трёх смежных точек.
Кубические полиномы затем состыковываются друг
с другом, чтобы образовать одну кривую.
Чтобы провести кубический сплайн через набор
точек:
- Создайте векторы vx и vy, содержащие
координаты x и y, через которые нужно
провести кубический сплайн. Элементы vx должны
быть расположены в порядке возрастания. (Хотя мы
используем имена vx, vy и vs, нет никаких
ограничений на имена этих переменных; можно
использовать любые имена.)
- Вычислите вектор vs := cspline( vx, vy).
Вектор vs содержит вторые производные
интеполяционной кривой в рассматриваемых
точках.
- Чтобы найти интерполируемое значение в
произвольной точке, скажем x0, вычислите interp(vs,
vx, vy, x0), где vs, vx и vy —
векторы, описанные ранее.
Обратите внимание, что можно сделать то же
самое, вычисляя:
interp(cspline( vx, vy), vx, vy, x0)
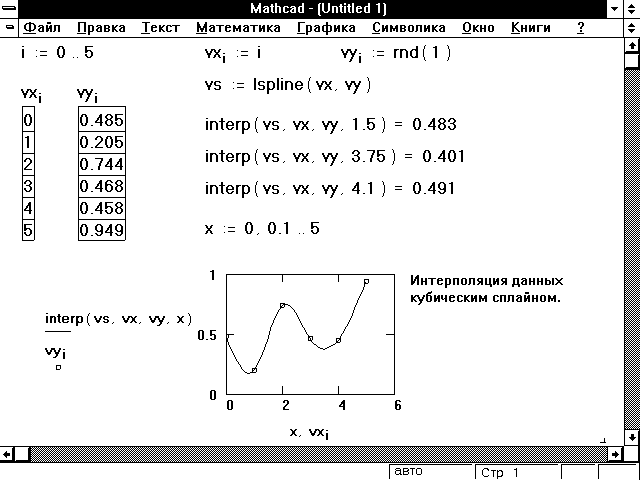
Рисунок 6: Пример сплайн-интерполяции.
На практике, возможно, придётся вычислять interp
во многих различных точках. Так как обращение к cspline
может требовать много времени, и так как
возвращаемый ею результат не зависит от
рассматриваемой точки, имеет смысл сделать
это один раз, сохранить результат и
многократно использовать, как описано выше.
Рисунок 6 показывает, как построить сплайн для
примера, приведенного на Рисунке 5. Описание
шагов, сделанных на Рисунке 6:
Выражение с функцией cspline вычисляет массив
вторых производных vs для сплайна,
используемого для интерполяции данных из vx и vy.
Как только массив vs найден, функция interp
вычисляет интерполируемые значения.
Обратите внимание, что массив vs должен
вычисляться только один раз, даже для
множественных интерполяций. Так как вычисление vs
требует много времени, лучше сохранять
промежуточные результаты в виде вектора, чем
повторно вычислять их по мере необходимости.
В дополнение к cspline Mathcad поставляется с
двумя другими кубическими сплайн-функциями. Три
сплайн-функции:
cspline(vx, vy)
pspline(vx, vy)
lspline(vx, vy) |
Они все возвращают вектор
коэффициентов вторых производных, который мы
будем называть vs. Этот вектор, vs, обычно
используется в функции interp, описанной ниже.
Аргументы vx и vy должны быть
вещественнозначными векторами одинаковой длины.
Значения в vx должны быть вещественны и
расположены в порядке возрастания. |
Они все возвращают вектор
коэффициентов вторых производных, который мы
будем называть vs. Этот вектор, vs, обычно
используется в функции interp, описанной ниже.
Аргументы vx и vy должны быть
вещественнозначными векторами одинаковой длины.
Значения в vx должны быть вещественны и
расположены в порядке возрастания.
Эти три функции отличаются только граничными
условиями: spline functions;end conditions for
- функция lspline генерирует кривую сплайна,
которая приближается к прямой линии в граничных
точках.
- функция pspline генерирует кривую сплайна,
которая приближается к параболе в граничных
точках.
- функция cspline генерирует кривую сплайна,
которая может быть кубическим полиномом в
граничных точках.
| interp (vs, vx, vy,
x) |
Возвращает интерполируемое
значение y, соответствующее аргументу x.
Вектор vs вычисляется на основе векторов
данных vx и vy одной из функций lspline, pspline
или cspline. |
Интерполируемое значение для
конкретного x есть ордината y
соответствующей точки сплайна. Для значений x,
расположенных перед первой точкой в vx, Mathcad
продолжает сплайн первой из составляющих его
кубических парабол. Для значений x,
расположенных за последней точкой в vx, Mathcad
продолжает сплайн последней из составляющих его
кубических парабол.
Для получения наилучших результатов значение x
должно находиться между самым большим и самым
маленьким значениями в векторе vx —
маловероятно, что будут полезны значения,
вычисленные для x вне этого диапазона.
Сплайны предназначены для интерполяции, а не
экстрaполяции.
Интерполяция вектора точек
Можно использовать оператор векторизации,
чтобы вычислить сразу целый набор
интерполируемых значений, соответствующих
вектору заданных точек. Это возможно и с interp,
и с linterp.
Рисунок 7 показывает, как выполнить эту
операцию. Чтобы применить оператор векторизации
к функции, щёлкните мышью на имени функции и
нажимайте [], пока в рамку не
попадёт нужная функция. Затем нажмите [Ctrl]-
(держите нажатой клавишу [Ctrl] и нажмите знак
минус).

Рисунок 7: Вычисление интерполируемых значений
в наборе точек.
Интерполяция сплайнами функций нескольких
переменных
Mathcad выполняет интерполяцию кубическими
сплайнами функции двух переменных тем же самым
образом, как и в одномерном случае, обсужденном
ранее. Mathcad проводит через сетку узлов
поверхность, составленную из кубических
полиномов от x и y, таким образом, что
первые и вторые частные производные являются
непрерывными в каждом узле сетки.
Первый шаг в двумерной сплайн-интерполяции —
точно такой же, как и в одномерном случае:
определить узлы, через которые поверхность
должна пройти. Однако это потребует больше
усилий, потому что теперь нужно определить сетку
узлов:
- Создайте n x 2 матрицу Mxy, чьи элементы Mxyi,0
и Mxyi,1 определяют x и y
координаты по диагонали прямоугольной сетки.
Эта матрица играет ту же самую роль, что и vx в
одномерном случае, описанном ранее. Так как эти
узлы описывают диагональ, элементы в каждом
столбце Mxy должны быть расположены в порядке
возрастания (Mxyi,k < Mxyj,k
всякий раз, когда i < j).
- Создайте n x n матрицу Mz, чей (ij)- элемент
есть координата z соответствующая точке x = Mxyi,0
и y = Mxyj,1. Она играет ту же самую роль,
что и vy в одномерном случае, описанном ранее.
- Вычислите вектор vs := cspline( Mxy, Mz).
Вектор vs содержит вторые производные
приближающей поверхности в узлах, определенных Mxy
и Mz.
- Чтобы найти интерполируемое значение в
произвольной точке, скажем ( x0, y0), вычислите
interp( vs, Mxy, Mz, 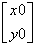 ) )
где vs, Mxy и Mz — массивы, описанные
ранее. Результатом является значение
интерполирующей функции, соответствующее точке (
x0, y0).
Обратите внимание, то же самое можно сделать,
вычисляя
interp( cspline( Mxy, Mz), Mxy,
Mz, 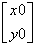 ) )
На практике, возможно, придётся вычислять interp
во многих различных точках. Так как обращение к cspline
может требовать много времени, и так как
возвращаемый ею результат не зависит от
рассматриваемой точки, имеет смысл сделать
это один раз, сохранить результат и
многократно использовать, как описано выше.
В дополнение к cspline Mathcad поставляется с
двумя другими функциями сплайн-интерполяции.
Функции сплайн-интерполяции Mathcad:
cspline(Mxy, Mz)
pspline(Mxy, Mz)
lspline(Mxy, Mz) |
Они все возвращают вектор
коэффициентов вторых производных, который мы
будем называть vs. Этот вектор, vs, обычно
используется в функции interp, описанной ниже. Mxy
— n x 2 матрица, чьи элементы Mxyi,0
и Mxyi,1 определяют точки на диагонали n x
n сетки. (ij)-элемент матрицы Mz
определяет значение интерполирующей функции
в ( Mxyi,0 , Mxyj,1). |
Эти три функции отличаются только
граничными условиями:
- Функция lspline генерирует сплайн, который
приближается к плоскости на краях сетки.
- функция pspline генерирует сплайн, который
представляет полином второй степени от x и y
на краях сетки.
- функция cspline генерирует сплайн, который
представляет полином третьей степени от x и y
на краях сетки.
| interp (vs, Mxy, Mz, v) |
Возвращает интерполируемое
значение z, соответствующее точкам x = v0
и y = v1. Вектор vs вычисляется
lspline, pspline, или cspline на основе данных из
Mxy и Mz. |
Для получения наилучших результатов не
используйте функцию interp для значений x и y,
удалённых от узлов сетки. Сплайны предназначены
для интерполяции, а не экстрaполяции, поэтому
маловероятно, что значения, вычисленные для
таких x и y, будут полезны.
Линейное предсказание
Функции интерполяции, описанные в этом
разделе до сих пор, позволяют по заданным
значениям некоторой функции в ряде точек оценить
её значения в промежуточных точках. Иногда
необходимо оценить значения функции в точках,
находящихся вне области расположения сетки, на
которой заданы значения функции. В Mathcad
есть функция predict, которая позволяет это
сделать. Эта функция использует линейный
алгоритм предсказания, который является
полезным, когда экстраполируемая функция
является гладкой и осциллирующей, хотя не
обязательно периодической. Линейное
предсказание можно рассматривать как
разновидность экстрaполяции, но его нельзя
путать с линейной или полиномиальной
экстрaполяцией.
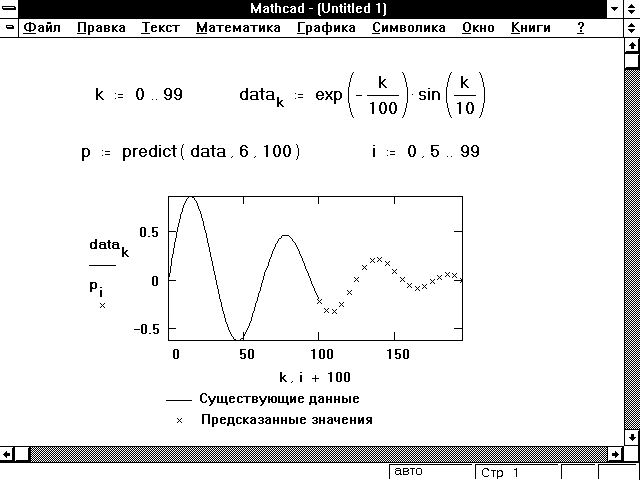
Рисунок 8: Использование функции предсказания
для экстраполяции данных.
| Е predict (v, m, n) |
Возвращает n предсказанных
значений, основанных на m последовательных
значениях вектора данных v. Элементы в v
должны представлять собой значения, взятые через
равные интервалы. |
Функция predict использует последние m
исходных значений данных, чтобы вычислить
коэффициенты предсказания. Как только это
сделано, она использует последние m точек,
чтобы предсказать координаты (m+1)-ой точки,
фактически создавая скользящее окно шириной в m
точек.
  
|

