Постановка задачи
приближенного решения уравнений ~ Этапы
решения задачи ~ Метод бисекций ~ Метод Ньютона ~ Метод простой
итерации
Пусть рассматривается уравнение 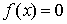 . Корнем уравнения называется значение . Корнем уравнения называется значение 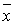 , при котором , при котором 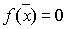 . Корень . Корень 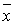 называется простым, если
называется простым, если
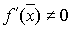 , в противном случае корень называется
кратным. Целое число m называется кратностью
корня , в противном случае корень называется
кратным. Целое число m называется кратностью
корня 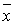 , если , если 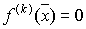 для k=1,2,3-,m-1 и для k=1,2,3-,m-1 и
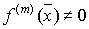 . .
Постановка задачи вычисления
приближенного значения корня с точностью 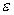 : найти такое значения : найти такое значения 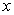 , что , что 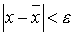 . .
Решение задачи разбивается на два этапа:
на первом этапе осуществляют локализацию
корней, на втором этапе производят итерационное
уточнение корней. На этапе локализации корней
находят достаточно узкие отрезки ( или отрезок,
если корень единственный), которые содержат один
и только один корень уравнения 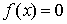 . На
втором этапе вычисляют приближенное значение
корня с заданной точностью. Часто вместо отрезка
локализации достаточно указать начальное
приближение к корню. . На
втором этапе вычисляют приближенное значение
корня с заданной точностью. Часто вместо отрезка
локализации достаточно указать начальное
приближение к корню.

ПРИМЕР 1. Локализация
корней.
Метод бисекции. Пусть [a,b] v
отрезок локализации. Предположим, что функция f(x)
непрерывна на [a,b] и на концах принимает значения
разных знаков 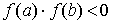 . .
Алгоритм метода бисекции состоит в
построении последовательности вложенных
отрезков, на концах которых функция принимает
значения разных знаков. Каждый последующий
отрезок получают делением пополам предыдущего.
Опишем один шаг итераций метода. Пусть на k-ом
шаге найден отрезок 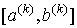 такой, что такой, что 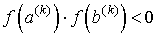 .
Найдем середину отрезка .
Найдем середину отрезка 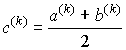 . Если . Если 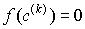 , то , то 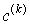 - корень и задача
решена. Если нет, то из двух половин отрезка
выбираем ту, на концах которой функция имеет
противоположные знаки: - корень и задача
решена. Если нет, то из двух половин отрезка
выбираем ту, на концах которой функция имеет
противоположные знаки:
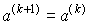 , , 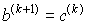 , если , если 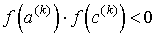
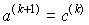 , , 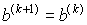 , если , если 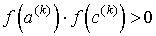
Критерий окончания итерационного процесса:
если длина отрезка локализации меньше 2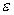 , то итерации прекращают и в качестве
значения корня с заданной точностью принимают
середину отрезка. , то итерации прекращают и в качестве
значения корня с заданной точностью принимают
середину отрезка.
Теорема о сходимости метода бисекций. Пусть
функция f(x) непрерывна на [a,b] и на концах
принимает значения разных знаков 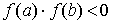 .Тогда
метод сходится и справедлива оценка погрешности
: .Тогда
метод сходится и справедлива оценка погрешности
: 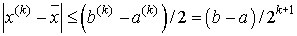

ПРИМЕР 2. Решение
уравнения методом бисекции.
Метод Ньютона (метод касательных) .
Расчетная формула метода Ньютона имеет вид:
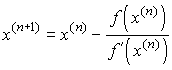 . Геометрически метод Ньютона
означает, что следующее приближение к корню . Геометрически метод Ньютона
означает, что следующее приближение к корню 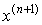 есть точка пересечения с осью ОХ есть точка пересечения с осью ОХ
касательной, проведенной к графику функции y=f(x)
в точке 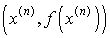 . .
Теорема о сходимости метода Ньютона.
Пусть 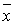 - простой корень уравнения - простой корень уравнения 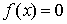 , в некоторой окрестности которого функция
дважды непрерывно дифференцируема. Тогда
найдется такая малая , в некоторой окрестности которого функция
дважды непрерывно дифференцируема. Тогда
найдется такая малая 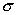 - окрестность корня - окрестность корня 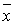 , что при произвольном выборе начального
приближения , что при произвольном выборе начального
приближения 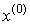 из этой окрестности
итерационная последовательность метода Ньютона
не выходит за пределы окрестности и справедлива
оценка из этой окрестности
итерационная последовательность метода Ньютона
не выходит за пределы окрестности и справедлива
оценка
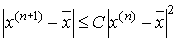 , где , где 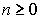 , , 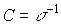 . .
Критерий окончания итерационного процесса.
При заданной точности 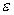 >0
вычисления следует вести до тех пор пока не
окажется выполненным неравенство >0
вычисления следует вести до тех пор пока не
окажется выполненным неравенство 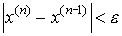 . .

ПРИМЕР 3. Решение
уравнения методом Ньютона.
Как указано в теореме, метод Ньютона обладает
локальной сходимостью, то есть областью его
сходимости является малая окрестность корня 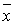 . Неудачный выбор может дать
расходящуюся итерационную последовательность. . Неудачный выбор может дать
расходящуюся итерационную последовательность.

ПРИМЕР 4.
Чувствительность метода Ньютона к выбору
начального приближения.
Метод простой итерации (метод
последовательных повторений). Для
применения метода простой итерации следует
исходное уравнение 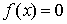 преобразовать к виду,
удобному для итерации преобразовать к виду,
удобному для итерации 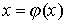 . Это
преобразование можно выполнить различными
способами. Функция . Это
преобразование можно выполнить различными
способами. Функция 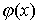 называется
итерационной функцией. Расчетная формула метода
простой итерации имеет вид: называется
итерационной функцией. Расчетная формула метода
простой итерации имеет вид: 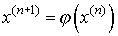 . .
Теорема о сходимости метода простой
итерации. Пусть в некоторой 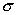 -
окрестности корня -
окрестности корня 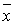 функция функция 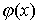 дифференцируема и удовлетворяет неравенству
дифференцируема и удовлетворяет неравенству 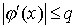 , где , где 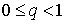 - постоянная . Тогда
независимо от выбора начального приближения из
указанной - постоянная . Тогда
независимо от выбора начального приближения из
указанной 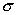 - окрестности итерационная
последовательность не выходит из этой
окрестности, метод сходится - окрестности итерационная
последовательность не выходит из этой
окрестности, метод сходится
со скоростью геометрической
последовательности и справедлива оценка
погрешности: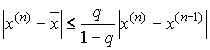 , , 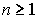 . .
Критерий окончания итерационного процесса.
При заданной точности 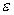 >0
вычисления следует вести до тех пор пока не
окажется выполненным неравенство >0
вычисления следует вести до тех пор пока не
окажется выполненным неравенство 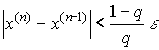 . Если
величина . Если
величина 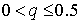 , то можно использовать
более простой критерий окончания итераций: , то можно использовать
более простой критерий окончания итераций: 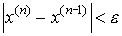 . .
Ключевой момент в применении метода простой
итерации состоит в эквивалентном преобразовании
уравнения. Способ, при котором выполнено условие
сходимости метода простой итерации, состоит в
следующем: исходное уравнение приводится к виду 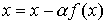 . Предположим дополнительно, что
производная . Предположим дополнительно, что
производная 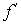 знакопостоянна и знакопостоянна и 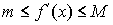 на отрезке [a,b]. Тогда при выборе
итерационного параметра на отрезке [a,b]. Тогда при выборе
итерационного параметра 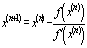 метод
сходится и значение метод
сходится и значение
 . .
ПРИМЕР 5.
Приведение уравнения к виду, удобному для
итераций.

|

