Если 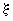 —
случайная величина с областью значений Xx , а функция f(x) определена
на множестве Xx , то h
= f(x) — тоже случайная величина. Задача об
отыскании функции распределения случайной
величины h по известной функции
распределения случайной величины x
легко решается, если f(x) — непрерывная
монотонно возрастающая функция. Доказано, что
тогда функция распределения Fh (x)
случайной величины h задается
формулой Fh (x) = Fx
([f(x)]-1). —
случайная величина с областью значений Xx , а функция f(x) определена
на множестве Xx , то h
= f(x) — тоже случайная величина. Задача об
отыскании функции распределения случайной
величины h по известной функции
распределения случайной величины x
легко решается, если f(x) — непрерывная
монотонно возрастающая функция. Доказано, что
тогда функция распределения Fh (x)
случайной величины h задается
формулой Fh (x) = Fx
([f(x)]-1).Здесь Fx (x)
— известная функция распределения случайной
величины 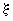 , а символом [f(x)]-1
обозначена функция, обратная к функции f(x). , а символом [f(x)]-1
обозначена функция, обратная к функции f(x).
Плотность распределения случайной величины h для дифференцируемой f(x)
находится по формуле
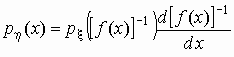 . .
Пример 1. Найдем плотность
вероятностей случайной величины h
= ex , где 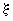 —
случайная величина, распределенная по
стандартному нормальному закону. —
случайная величина, распределенная по
стандартному нормальному закону.
В теории вероятностей часто возникает
необходимость в определении плотности
вероятности суммы двух независимых случайных
величин. Доказано, что если 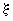 1 и 1 и 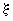 2 —независимые непрерывные
случайные величины с плотностями вероятности
соответственно p1(x) и p2(x),
то плотность вероятностей суммы h = 2 —независимые непрерывные
случайные величины с плотностями вероятности
соответственно p1(x) и p2(x),
то плотность вероятностей суммы h =
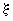 1 + 1 + 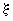 2 —
свертка плотностей вероятностей слагаемых, т.е.
вычисляется по формуле: 2 —
свертка плотностей вероятностей слагаемых, т.е.
вычисляется по формуле:
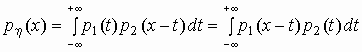 . .
Пример 2. Найдем плотность
вероятности суммы двух стандартных нормальных
распределений случайных величин h
= 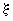 1 + 1 + 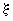 2 и h = 2 и h = 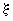 1 + 1 + 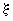 1 = 2 1 = 2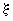 1 , где 1 , где 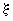 1 и 1 и 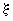 2 — независимые случайные величины
со стандартным нормальным распределением. 2 — независимые случайные величины
со стандартным нормальным распределением.
Пример 3. Найдем распределение
произведения компонент двумерного дискретного
случайного вектора с по известным
распределениям его компонент.
Замечание. Вычисления в примере 3 проще
произвести на бумаге. Использовать компьютер
бессмысленно.
Пусть (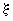 , h ) —
дискретный случайный вектор с распределением: , h ) —
дискретный случайный вектор с распределением:
| |
1 |
2 |
3 |
4 |
| 0 |
0.01 |
0.02 |
0.03 |
0.04 |
| 1 |
0.1 |
0.1 |
0.2 |
0.4 |
| 2 |
0.05 |
0.01 |
0.01 |
0.03 |
Найдем распределение случайной величины z = 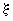 h. h.
Очевидно, что случайная величина z
= 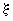 h принимает значения
0, 1, 2, 3, 4, 6, 8. h принимает значения
0, 1, 2, 3, 4, 6, 8.
Вычислим соответствующие вероятности:
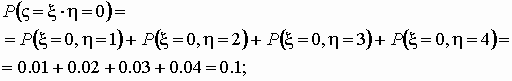
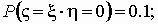
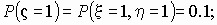
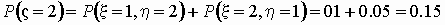 и т.д. и т.д.
В результате получим распределение случайной
величины 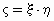 : :
| z |
0 |
1 |
2 |
3 |
4 |
6 |
8 |
| p |
0.1 |
0.1 |
0.15 |
0.2 |
0.41 |
0.01 |
0.03 |

|

