| Если две случайные величины x и h зависимы, то
информация о том, какое значение приняла одна из
них меняет наше представление о распределении
другой. Иначе говоря, по распределению
двумерной случайной величины (x , h ) можно судить о распределении
каждой из величин x и h
.
Пусть дана двумерная случайная величина (x , h ) с распределением
| |
y1 |
y2 |
… |
yn |
| x1 |
p11 |
p12 |
... |
p1n |
| x2 |
p21 |
p22 |
... |
p2n |
| … |
... |
... |
... |
... |
| xn |
pn1 |
pn2 |
... |
pnn |
Тогда распределения случайных величин x и h имеют вид
| x |
x1 |
x2 |
... |
xn |
| p |
p1. |
p2. |
... |
pn. |
| h |
y1 |
y2 |
... |
yn |
| p |
p.1 |
p.2 |
... |
p.n |
Здесь точка в индексе означает соответственно
суммирование по строкам и по столбцам:
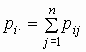 , , 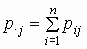 . .
Условным распределением случайной
величины x при условии, что
случайная величина h приняла
значение h = yj, называется
распределение:
Нетрудно убедиться, что сумма вероятностей
величины x в этом распределении
равна единице.
Аналогично условным распределением случайной
величины h при условии, что
случайная величина x приняла
значение x = xi, называется
распределение:
Рассмотрим пример, поясняющий понятие
условного распределения.
ПРИМЕР 1. Найдем распределение
каждой компоненты и условные распределения
компонент двумерной случайной величины по
заданному распределению двумерной случайной
величины.

|

