Понятие
случайного вектора ~ Функция
распределения случайного вектора ~ Плотность
совместного распределения ~ Совместное
распределение дискретных величин
Понятие случайного вектора.
В одном и том же случайном эксперименте можно
рассматривать не одну, а несколько - n функций,
аргументом которых являются случайные события.
Совокупность таких функций называется многомерной
случайной величиной или случайным вектором
и обозначается
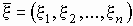 . .
Функцией распределения случайного
вектора или совместным распределением
случайных величин x 1, x 2, …, x n
называется вероятность
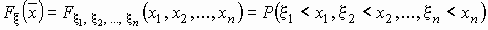 , ,
где 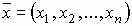 . .
По многомерной функции можно найти
распределение каждой из компонент x
1, x 2, …, x
n. Например, если 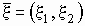 - двумерная случайная величина, имеющая
совместное распределение Fx
1, x 2
(x1, x2), то функции
распределения компонент Fx 1
(x1) и F x 2(x2)
вычисляются по формулам
- двумерная случайная величина, имеющая
совместное распределение Fx
1, x 2
(x1, x2), то функции
распределения компонент Fx 1
(x1) и F x 2(x2)
вычисляются по формулам
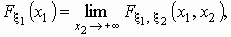 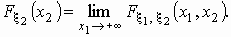
В дальнейшем будем рассматривать только
двумерные случайные величины.
Плотность совместного распределения
Случайный вектор 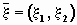 называется непрерывным случайным вектором,
если существует такая неотрицательная функция
называется непрерывным случайным вектором,
если существует такая неотрицательная функция 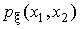 , что для любого
прямоугольника W на плоскости
(x1, x2), вероятность события , что для любого
прямоугольника W на плоскости
(x1, x2), вероятность события 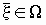 равна равна
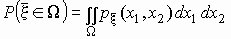 . .
Функция 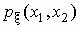 в этом
случае называется совместной плотностью
распределения. в этом
случае называется совместной плотностью
распределения.
Легко показать, что
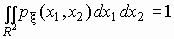 . .
Плотности вероятностей компонент случайного
вектора вычисляются по формулам 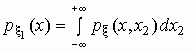 , ,  . .
ПРИМЕР 1 . Распределение
координат непрерывного случайного вектора.
Совместное распределение дискретных
величин
Если (x , h ) -
дискретный случайный вектор, то совместным
распределением случайных величин x
и h чаще всего называют таблицу
вида
| |
y1 |
y2 |
... |
ym |
x1 |
p11 |
p12 |
... |
y1m |
x2 |
p21 |
p22 |
... |
p2m |
... |
... |
... |
pij |
... |
xn |
pn1 |
pn2 |
... |
pnm |
где xi и yj - значения x и h соответственно,
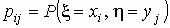 и и 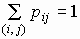 . .
По этой таблице можно найти распределение
каждой из случайных величин x и h по формулам:
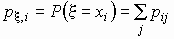 , ,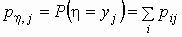 . .
ПРИМЕР 2 . Распределение
координат дискретного случайного вектора.

|

