Ковариация ~ Корреляция
Ковариация
Если между случайными величинами 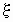 и и 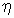 существует стохастическая связь, то
одним из параметров, характеризующих меру этой
связи является ковариация существует стохастическая связь, то
одним из параметров, характеризующих меру этой
связи является ковариация 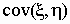 . Ковариацию вычисляют по формулам . Ковариацию вычисляют по формулам
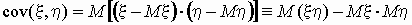 . .
Если случайные величины 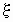 и и 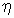 независимы,
то независимы,
то 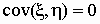 . .
Обратное, вообще говоря, неверно. Из равенства
нулю ковариации не следует независимость
случайных величин. Случайные величины могут быть
зависимыми в то время как их ковариация —
нулевая!
Но зато, если ковариация случайных величин
отлична от нуля, то между ними существует
стохастическая связь, мерой которой и является
величина ковариации.
Интересно отметить, что 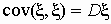 и и 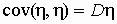 . .
Кроме того, важны следующие свойства
ковариации:
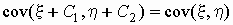 ; ;
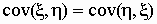 ; ;
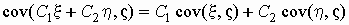 . .
Ковариационной матрицей случайного вектора 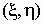 называется
матрица вида называется
матрица вида
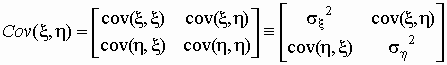 . .
Эта матрица симметрична и положительно
определена. Ее определитель называется обобщенной
дисперсией и может служить мерой рассеяния
системы случайных величин 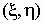 . .
Как уже отмечалось ранее, дисперсия суммы независимых
случайных величин равна сумме их дисперсий: 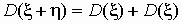 . .
Если же случайные величины зависимы, то
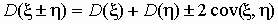 . .
Пример 1. Вычислим ковариации
компонент дискретного случайного вектора 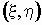 , заданного
распределением , заданного
распределением
Корреляция
Понятно, что значение ковариации зависит не
только от “тесноты” связи случайных величин, но
и от самих значений этих величин, например, от
единиц измерения этих значений.
Для исключения этой зависимости вместо
ковариации используется коэффициент
корреляции 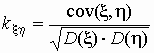 . .
Этот коэффициент обладает следующими
свойствами:
он безразмерен;
его модуль не превосходит единицы, т.е. 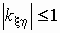 ; ;
если 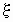 и и 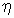 независимы, то независимы, то 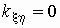 (обратное, вообще говоря
неверно!); (обратное, вообще говоря
неверно!);
если 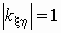 , то
случайные величины , то
случайные величины 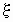 и и 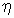 связаны функциональной
зависимостью вида связаны функциональной
зависимостью вида 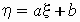 ,
где ,
где 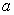 и и
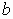 — некоторые
числовые коэффициенты; — некоторые
числовые коэффициенты;
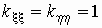 ; ;
Корреляционной матрицей случайного вектора называется
матрица
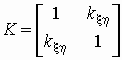 . .
Если 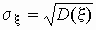 и и 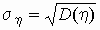 , то ковариационная и
корреляционная матрицы случайного вектора , то ковариационная и
корреляционная матрицы случайного вектора 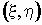 связаны соотношением связаны соотношением
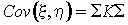 , ,
где 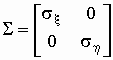 . .
Пример 2. Вычислим
корреляционную матрицу дискретного случайного
вектора из примера 1.

|

