Математическое
ожидание ~ Дисперсия ~ Условное
математическое ожидание
Математическое ожидание
Пусть 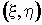 — двумерная
случайная величина, тогда — двумерная
случайная величина, тогда 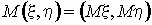 , т.е. математическое ожидание
случайного вектора — это вектор из
математических ожиданий компонент вектора. , т.е. математическое ожидание
случайного вектора — это вектор из
математических ожиданий компонент вектора.
Если 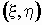 — дискретный
случайный вектор с распределением — дискретный
случайный вектор с распределением
| |
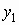 |
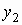 |
... |
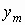 |
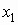 |
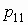 |
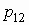 |
... |
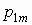 |
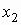 |
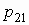 |
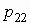 |
... |
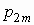 |
| ... |
... |
... |
... |
... |
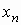 |
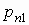 |
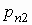 |
... |
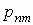 |
то математические ожидания компонент
вычисляются по формулам:
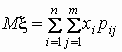 , , 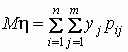 . .
Эти формулы можно записать в сокращенном виде.
Обозначим
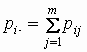 и и 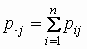 , ,
тогда
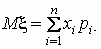 и и 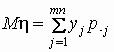 . .
Эти формулы естественно обобщаются на
непрерывный случай.
Если 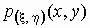 — совместная
плотность распределения двумерной случайной
величины — совместная
плотность распределения двумерной случайной
величины 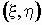 , то , то
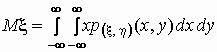 и и 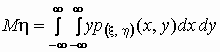 . .
Поскольку
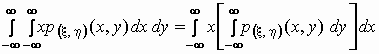
и 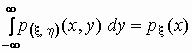 — не что иное как
плотность распределения случайной величины, то — не что иное как
плотность распределения случайной величины, то 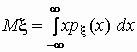 и, аналогично, и, аналогично, 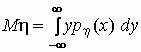 . .
Пример 1. Вычислим
математическое ожидание дискретного двумерного
случайного вектора с распределением
| |
0 |
1 |
2 |
| 2 |
0.1 |
0.1 |
0.2 |
| 7 |
0.2 |
0.2 |
0.2 |
Дисперсия
Понятие дисперсии нетривиальным образом
обобщается на многомерные случайные величины.
Это обобщение будет сделано в следующем разделе.
Здесь лишь приведем формулы для вычисления
дисперсии компонент двумерного случайного
вектора.
Если 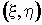 — двумерная
случайная величина, то — двумерная
случайная величина, то
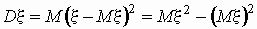 , , 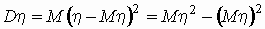 . .
Входящие в эту формулу математические ожидания
вычисляются по приведенным выше формулам.
Пример 2. Вычислим дисперсию
двумерного случайного вектора, определенного в
примере 1.
Условное математическое ожидание
Между случайными величинами может
существовать функциональная зависимость.
Например, если 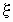 —
случайная величина и —
случайная величина и 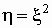 ,
то ,
то 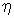 — тоже случайная
величина, связанная с — тоже случайная
величина, связанная с 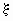 функциональной зависимостью. В то же время между
случайными величинами может существовать
зависимость другого рода, называемая стохастической.
В разделе, посвященном условным
распределениям уже обсуждалась такая
зависимость. Из рассмотренных там примеров ясно
видно, что информация о значении одной случайной
величины (одной компоненты случайного вектора)
изменяет распределение другой случайной
величины (другой компоненты случайного вектора),
а это может, вообще говоря, изменить и числовые
характеристики случайных величин.
функциональной зависимостью. В то же время между
случайными величинами может существовать
зависимость другого рода, называемая стохастической.
В разделе, посвященном условным
распределениям уже обсуждалась такая
зависимость. Из рассмотренных там примеров ясно
видно, что информация о значении одной случайной
величины (одной компоненты случайного вектора)
изменяет распределение другой случайной
величины (другой компоненты случайного вектора),
а это может, вообще говоря, изменить и числовые
характеристики случайных величин.
Математическое ожидание, вычисленной по
условному распределению, называется условным
математическим ожиданием.
Для двумерного дискретного случайного вектора 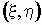 с распределением с распределением
| |
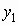 |
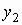 |
... |
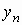 |
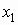 |
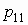 |
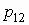 |
... |
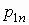 |
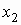 |
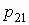 |
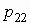 |
... |
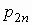 |
| ... |
... |
... |
... |
... |
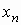 |
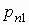 |
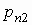 |
... |
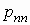 |
условное математическое ожидание случайной
величины 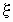 при условии,
что случайная величина при условии,
что случайная величина 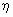 принимает значение принимает значение 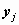 , вычисляется по
формуле , вычисляется по
формуле
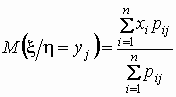 . .
Аналогично, условное математическое ожидание
случайной величины 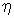 при условии, что случайная величина
при условии, что случайная величина 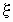 принимает значение принимает значение 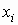 , равно , равно
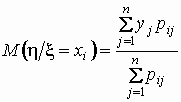 . .
Пример 3. Вычислим
математические ожидания и условные
математические ожидания компонент случайного
вектора 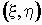 , заданного
распределением, , заданного
распределением,
| |
1 |
2 |
3 |
1 |
0.1 |
0.1 |
0.2 |
2 |
0.2 |
0.2 |
0.2 |
Видно, что условное математическое ожидание
случайной величины 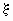 является функцией значений случайной величины
является функцией значений случайной величины 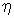 , т.е. , т.е.
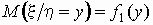
и, совершенно аналогично,
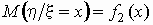 . .
Функцию 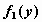 называют регрессией случайной величины
называют регрессией случайной величины 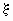 на случайную величину на случайную величину 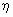 , а , а 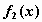 — регрессией случайной величины — регрессией случайной величины 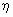 на случайную величину на случайную величину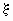 . .
Формулы условных математических ожиданий для
дискретных случайных величин естественным
образом обобщаются на непрерывные случайные
величины.
Если 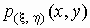 совместная
плотность вероятностей двумерной случайной
величины совместная
плотность вероятностей двумерной случайной
величины 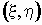 , то , то
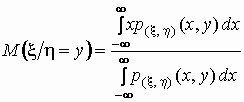 и и 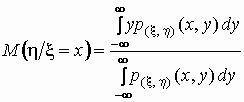 . .
Рассмотрим непрерывный случайный вектор 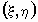 с плотностью
распределения с плотностью
распределения
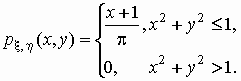
Нетрудно проверить, что 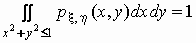 . .
Найдем распределения компонент случайного
вектора и их математические ожидания и условные
математические ожидания:
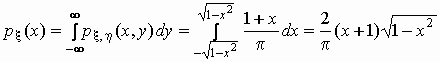 , ,
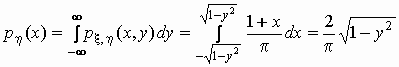 , ,
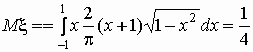 , , 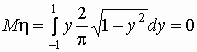 , ,
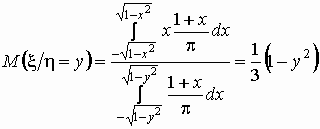 , , 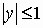 , , 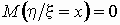 . .
В этом случае регрессия 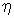 на на 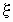 равна
нулю, а регрессия равна
нулю, а регрессия 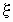 на на 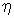 описывается уравнением описывается уравнением
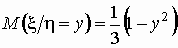 . .

|

