Целая положительная степень комплексного числа ~ Корень n-степени ~ Экспонента ~ Тригонометрические функции ~ Гиперболические функции ~ Логарифм ~ Показательная и степенная функции ~ Обратные тригонометрические функции

Значение целой положительной степени комплексного аргумента, значение функции f(z) = z ⁿ , проще всего вычислять в тригнометрической форме.
Если z = x + iy = r  (cosj  + isinj ), то для любого целого положительного числа n имеет место формула:
w = f(z) = z ⁿ =  r  ⁿ (cos nj  + isin nj ).
Если w = f (z) =  f (x + iy) = u(x, y) + iv(x, y), то
u(x, y) = r  ⁿcos nj , u(x, y) = r  ⁿsin nj.

ПРИМЕР 1. Вычисление f(z) = zⁿ.

Корнем n-й степени из комплексного числа z называется число
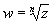 такое, что wⁿ = z.
Для любого комплексного числа z существует n комплексных чисел w таких, что wⁿ = z.
Значение корня, т.е. значение функции

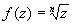
проще всего вычислять в тригнометрической форме.
Если z = x + iy = r (cosj + isinj), то для любого целого положительного числа n имеет место формула:

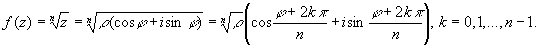
Т.е. функция

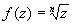
является многозначной функцией ^_ каждому значению аргумента отвечает n различных значений корня.

Если w = f(z) =  f(x + iy) = u(x, y) + iv(x, y), то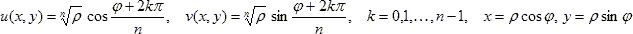
ПРИМЕР 2. Вычисление корня n-й степени из комплексного числа.

Если z = x + iy = r  (cosj + isinj ), то значения функции f(z) = exp(z) вычисляются по формуле
f(z) = e^z = e^x+iy = e ^xe ^iy = e^x (cosy + isiny).
Если w = f(z) =  f(x + iy) = u(x, y) + iv(x, y), то
u(x,y) = e^x cosy , v(x,y) = e^x siny.

ПРИМЕР 3. Вычисление значения функции exp(z).

Тригонометрические функции комплексного аргумента определяются формулами:

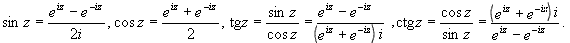
ПРИМЕР 4. Вычисление значений тригонометрических функций комплексного переменного.

Гиперболические функции комплексного переменного определяются совершенно так же, как функции в действительной области:

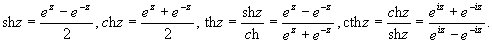
ПРИМЕР 5. Вычисление значений гиперболических функций комплексного переменного.

Логарифмом комплексного числа z называется такое число w, что
exp(w) = z.
Значения логарифмической функции f(z) = Ln(z) вычисляются по формуле
Ln(z) = ln(|z|) + iArg z = ln(|z|) + iarg z + 2kp i,  k = 0,1,2,...
Величину ln(|z|) + iarg z называют главным значением логарифма.
Функция f(z) = Ln(z) является многозначной функцией ^_ каждому значению аргумента отвечает бесконечное множество различных значений логарифма.

ПРИМЕР 6. Вычисление значений логарифма комплексного числа.

Показательная (f(z) = a^z) и степенная (f(z) = z^a) функции комплексного переменного определяются с помощью логарифма -    для любых комплексных чисел a и z справедливо:
f(z) = a^z = e^zLna;
f(z) = z^a= e^aLnz.

ПРИМЕР 7. Вычисление значений показательной и степенной функций комплексного переменного.

Значения обратных тригонометрических функций комплексного переменного вычисляются по формулам:
.

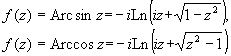ПРИМЕР 8. Вычисление значений обратных тригонометрических функций комплексного переменного.