Определение комплексного числа ~ Геометрическая итерпретация комплексного числа
Тригонометрическая форма  ~ Показательная форма ~ Модуль и аргумент комплексного числа ~ Арифметические операции с комплексными числами

Комплексным числом z называется упорядоченная пара действительных чисел x и y.
Первое из них x называется действительной частью комплексного числа z и обозначается Rez, x = Rez;
второе число y называется мнимой частью комплексного числа z и обозначается Imz, y = Imz.
Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части:

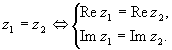
Алгебраическая форма записи комплексного числа

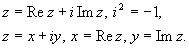
Число
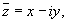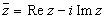  ,   где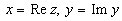 
называется комплексно сопряженным числу
  

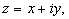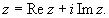
Комплексное число z = x + iy естественно изображать в виде точки на плоскости с декартовыми координатами (x, y).

Если x и y - декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, j) и воспользовавшись связью
x = rcosj, y = rsinj
получим тригонометрическую форму записи комплексного числа:
z = r (cosj + isinj) .
При этом число r называют модулем комплексного числа, |z| = r, а число j - аргументом комплексного числа,
Arg z = arg z+2kp= j.

При решении задач для вычисления аргумента удобно пользовааться схемой, приведенной ниже:

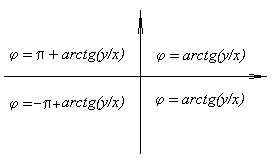
Справедливы соотношения:

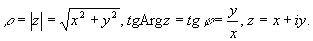
Используя формулу Эйлера

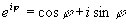
получим показательную форму записи комплексного числа:

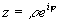
ПРИМЕР 1. Различные формы представления комплексного числа. Геометрическая интерпретация комплексных чисел.

Арифметические операции c комплексными числами определяются следующим образом:
если

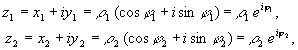
то

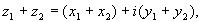
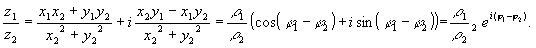
ПРИМЕР 2. Арифметические операции с комплексными числами.