Потенциальное поле ~ Условие
потенциальности поля ~ Вычисление
потенциала векторного поля
Потенциальное поле. Если векторное
поле 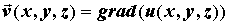 , то оно называется потенциальным,
а скалярное поле , то оно называется потенциальным,
а скалярное поле 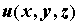 , соответственно, его потенциалом.
Самым известным примером такого соответствия
является электрическое поле, напряженность
которого , соответственно, его потенциалом.
Самым известным примером такого соответствия
является электрическое поле, напряженность
которого 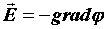 , где , где 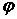 - потенциал электрического поля.
Минус в формуле связан с историческим выбором
направления вектора напряженности от плюса к
минусу, когда уже умели тереть шерсть об янтарь,
но не знали, как это описывать математически. - потенциал электрического поля.
Минус в формуле связан с историческим выбором
направления вектора напряженности от плюса к
минусу, когда уже умели тереть шерсть об янтарь,
но не знали, как это описывать математически.
ПРИМЕР 1. Исследование
потенциального поля.
Условие потенциальности поля. Пусть
задано скалярное поле 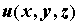 , причем данная
функция дважды непрерывно дифференцируема.
Напомним, что в этом случае смешанные частные
производные второго порядка не зависят от
порядка дифференцирования. Вычислим , причем данная
функция дважды непрерывно дифференцируема.
Напомним, что в этом случае смешанные частные
производные второго порядка не зависят от
порядка дифференцирования. Вычислим 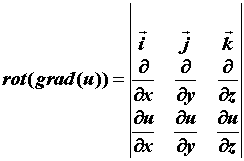 . .
Нетрудно видеть, что при этих условиях
получается тождественный ноль. То есть, если поле
потенциальное, то его 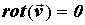 . .
ПРИМЕР 2. Проверка
потенциальности поля.

Вычисление потенциала векторного поля.
Если мы убедились, что поле 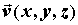 является
потенциальным, то есть его ротор равен нулю, то
представляет интерес вычислить потенциал этого
поля. Для этого рассмотрим криволинейный
интеграл в данном векторном поле: является
потенциальным, то есть его ротор равен нулю, то
представляет интерес вычислить потенциал этого
поля. Для этого рассмотрим криволинейный
интеграл в данном векторном поле: 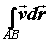 , где точки А и В -
начальная и конечная точки кривой. Поскольку , где точки А и В -
начальная и конечная точки кривой. Поскольку 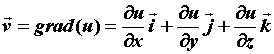 , то
скалярное произведение векторов , то
скалярное произведение векторов 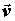 и и
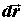 является полным
дифференциалом функции является полным
дифференциалом функции 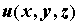 : : 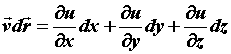 . Поэтому из
свойств криволинейного интеграла следует, что . Поэтому из
свойств криволинейного интеграла следует, что 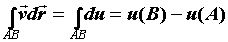 . Смысл
полученной формулы состоит в том, что работа поля
по перемещению материальной точки из А в В не
зависит от пути интегрирования, а только от
конечной и начальной точек, точнее, от разности
потенциалов в этих точках. Понятие разности
потенциалов хорошо известно из физики. Для
вычисления потенциала поля в произвольной точке
В выберем начальную точку А, от которой начнем
отсчет (в физике часто это - бесконечно удаленная
точка). Тогда . Смысл
полученной формулы состоит в том, что работа поля
по перемещению материальной точки из А в В не
зависит от пути интегрирования, а только от
конечной и начальной точек, точнее, от разности
потенциалов в этих точках. Понятие разности
потенциалов хорошо известно из физики. Для
вычисления потенциала поля в произвольной точке
В выберем начальную точку А, от которой начнем
отсчет (в физике часто это - бесконечно удаленная
точка). Тогда 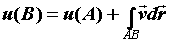 . Поскольку интеграл не зависит от
пути интегрирования, то выберем его так, как нам
удобно: сначала параллельно оси 0х, потом
параллельно 0у, наконец, параллельно 0z. Обозначая . Поскольку интеграл не зависит от
пути интегрирования, то выберем его так, как нам
удобно: сначала параллельно оси 0х, потом
параллельно 0у, наконец, параллельно 0z. Обозначая 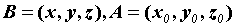 ,
получим: ,
получим:
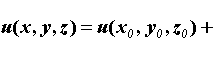
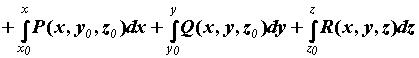 . .
Здесь 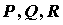 - компоненты векторного поля - компоненты векторного поля
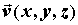 . Поскольку выбор начальной точки
произволен, потенциал поля определяется с
точностью до произвольной постоянной, которая
определяется физическими соображениями. . Поскольку выбор начальной точки
произволен, потенциал поля определяется с
точностью до произвольной постоянной, которая
определяется физическими соображениями.
ПРИМЕР 3. Вычисление
потенциала векторного поля.

|

