Формула Стокса ~ Ротор
векторного поля
Формула Стокса. Рассмотрим в
пространстве кусок двухсторонней
кусочно-гладкой поверхности 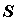 , край которой
образуется кусочно-гладкой кривой , край которой
образуется кусочно-гладкой кривой 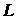 . Выберем
положительную сторону поверхности (из конца
единичного вектора нормали . Выберем
положительную сторону поверхности (из конца
единичного вектора нормали 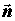 обход
границы представляется против часовой стрелки).
Для циркуляции векторного поля обход
границы представляется против часовой стрелки).
Для циркуляции векторного поля 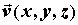 вдоль контура границы имеет место формула
Стокса:
вдоль контура границы имеет место формула
Стокса: 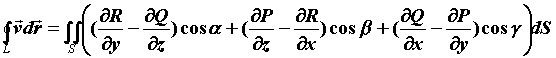 , где , где 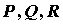 - компоненты
векторного поля, - компоненты
векторного поля, 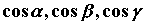 - направляющие
косинусы вектора нормали. - направляющие
косинусы вектора нормали.
ПРИМЕР 1. Вычисление
циркуляции по формуле Стокса.
Ротор векторного поля. Рассмотрим в
пространстве замкнутый контур 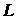 с выбранным
направлением обхода, лежащий в ориентированной
плоскости на ее положительной стороне (из конца
единичного вектора нормали с выбранным
направлением обхода, лежащий в ориентированной
плоскости на ее положительной стороне (из конца
единичного вектора нормали 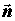 обход контура
представляется против часовой стрелки). Ротором обход контура
представляется против часовой стрелки). Ротором
 (или вихрем) векторного поля в
точке (или вихрем) векторного поля в
точке 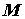 называется вектор, проекция
которого на направление вектора нормали есть называется вектор, проекция
которого на направление вектора нормали есть
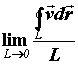 . Точка лежит . Точка лежит 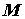 на плоскости
внутри контура на плоскости
внутри контура 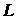 , который стягивается в эту точку
при вычислении предела. Поскольку ротор поля
определяется через циркуляцию, то он тоже
является мерой завихренности поля. Найдем
компоненты ротора в декартовой системе
координат, воспользовавшись формулой Стокса. Для
этого выберем сначала координатную плоскость y0z
с нормальным вектором , который стягивается в эту точку
при вычислении предела. Поскольку ротор поля
определяется через циркуляцию, то он тоже
является мерой завихренности поля. Найдем
компоненты ротора в декартовой системе
координат, воспользовавшись формулой Стокса. Для
этого выберем сначала координатную плоскость y0z
с нормальным вектором 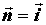 , затем x0z, , затем x0z,
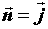 , затем x0y, , затем x0y, 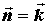 . Применяя каждый
раз теорему о среднем для интеграла, получим: . Применяя каждый
раз теорему о среднем для интеграла, получим:
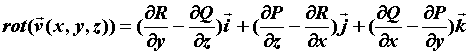
Теперь теорема Стокса может быть
сформулирована следующим образом: циркуляция
векторного поля вдоль контура равна потоку
ротора поля через поверхность, натянутую на этот
контур. Выражение для ротора поля проще
запомнить, если записать его в виде определителя:
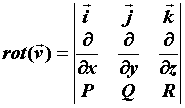 .
Используя свойства частных производных и
определителей, получим следующие свойства
ротора векторного поля: .
Используя свойства частных производных и
определителей, получим следующие свойства
ротора векторного поля:
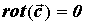
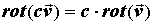
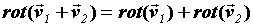
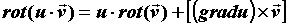
ПРИМЕР 2. Вычисление ротора
векторного поля.

|

