Криволинейный интеграл в
векторном поле ~ Циркуляция векторного
поля
Криволинейный интеграл в векторном поле.
Пусть заданы некоторое векторное поле 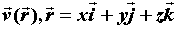 и
кривая АВ (А - начальная точка, В - конечная).
Криволинейный интеграл в векторном поле и
кривая АВ (А - начальная точка, В - конечная).
Криволинейный интеграл в векторном поле  есть скаляр, полученный следующим образом:
есть скаляр, полученный следующим образом:
Разобьем кривую точками А=А0, А1, А2-Аn=В
на n частей, приближенно изображаемых векторами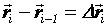 (разбиение
(разбиение 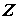 ). ).
Обозначим 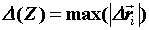 . .
На границе или внутри каждой элементарной дуги
Аi-1Ai выберем точку, которой
соответствует радиус-вектор 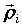 и составим
интегральную сумму и составим
интегральную сумму 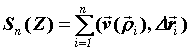 . .
Если существует 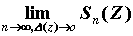 и он не
зависит от разбиения и он не
зависит от разбиения 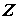 и выбора точек, то
этот предел называется криволинейным интегралом
в векторном поле. В декартовой системе координат: и выбора точек, то
этот предел называется криволинейным интегралом
в векторном поле. В декартовой системе координат:
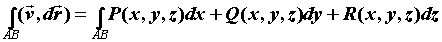 , где , где 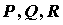 -
компоненты векторного поля. -
компоненты векторного поля.
Если кривая задана в параметрической форме:
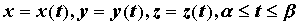 , то
вычисление криволинейного интеграла сводится к
определенному интегралу: , то
вычисление криволинейного интеграла сводится к
определенному интегралу:
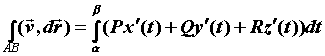 .
Используя определение и формулу для вычисления
нетрудно получить свойства криволинейного
интеграла: .
Используя определение и формулу для вычисления
нетрудно получить свойства криволинейного
интеграла:
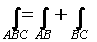
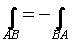
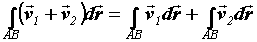
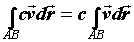
Подчеркнем, что, в отличие от криволинейного
интеграла по длине дуги, криволинейный интеграл
в векторном поле меняет знак при изменении
направления интегрирования.
Если 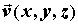 векторное поле, описывающее
физическое силовое поле, то криволинейный
интеграл выражает работу, которую совершает векторное поле, описывающее
физическое силовое поле, то криволинейный
интеграл выражает работу, которую совершает 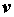 сила
при переносе материальной точки из пункта А в
пункт В вдоль кривой АВ. сила
при переносе материальной точки из пункта А в
пункт В вдоль кривой АВ.
ПРИМЕР 1. Вычисление
криволинейного интеграла в векторном поле.
Циркуляция векторного поля. Важной
характеристикой векторного поля является
циркуляция векторного поля, которая равна
криволинейному интегралу по замкнутой кривой в
области поля, или, как говорят, по замкнутому
контуру: 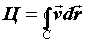 . Циркуляция векторного поля
является скалярной величиной и характеризует
вихревые свойства поля. Если в некоторой области
поля циркуляция равна нулю, то поле называют
безвихревым. . Циркуляция векторного поля
является скалярной величиной и характеризует
вихревые свойства поля. Если в некоторой области
поля циркуляция равна нулю, то поле называют
безвихревым.
ПРИМЕР 2. Вычисление
циркуляции векторного поля.

|

