Поток векторного поля через
замкнутую поверхность ~ Формула
Остроградского ~ Дивергенция
векторного поля
Поток векторного поля через замкнутую
поверхность. Рассмотрим кусочно-гладкую
двухстороннюю замкнутую ориентированную
поверхность 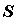 . Поток векторного поля . Поток векторного поля 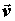 через
замкнутую поверхность через
замкнутую поверхность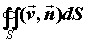 является важной
характеристикой поля и позволяет судить о
наличии источников и стоков поля. При
непосредственном вычислении потока через
замкнутую поверхность приходится разбивать ее
на части, однозначно проектируемые на
координатные плоскости. является важной
характеристикой поля и позволяет судить о
наличии источников и стоков поля. При
непосредственном вычислении потока через
замкнутую поверхность приходится разбивать ее
на части, однозначно проектируемые на
координатные плоскости.
ПРИМЕР 1. Непосредственное вычисление
потока через замкнутую поверхность.
Формула Остроградского. Пусть
замкнутая поверхность 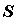 ограничивает
некоторый объем ограничивает
некоторый объем 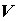 . Тогда в декартовых координатах
справедлива формула Остроградского: . Тогда в декартовых координатах
справедлива формула Остроградского: 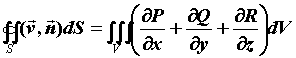 , где , где 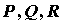 -
компоненты векторного поля. -
компоненты векторного поля.
ПРИМЕР 2. Вычисление потока
через замкнутую поверхность по формуле
Остроградского.
Дивергенция векторного поля.
Дивергенцией 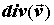 векторного поля векторного поля 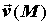 называется называется 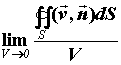 .
Точка .
Точка 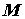 находится внутри замкнутой
поверхности находится внутри замкнутой
поверхности 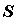 , ограничивающей объем , ограничивающей объем 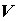 ,
который при вычислении предела стягивается в эту
точку. ,
который при вычислении предела стягивается в эту
точку. 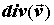 является скалярной величиной и
служит мерой источников поля. Если в некоторой
области поля является скалярной величиной и
служит мерой источников поля. Если в некоторой
области поля 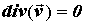 , то источников поля в этой области
нет. Такое поле называют соленоидальным.
Используя формулу Остроградского, нетрудно
получить выражение для вычисления дивергенции в
декартовых координатах: , то источников поля в этой области
нет. Такое поле называют соленоидальным.
Используя формулу Остроградского, нетрудно
получить выражение для вычисления дивергенции в
декартовых координатах: 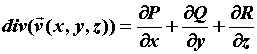 . Из свойств
частных производных следуют свойства
дивергенции векторного поля: . Из свойств
частных производных следуют свойства
дивергенции векторного поля:
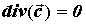
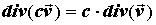
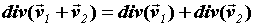
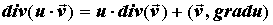
ПРИМЕР 3. Вычисление
дивергенции векторного поля.

|

