Поток векторного поля ~ Непосредственное вычисление потока
Поток векторного поля. Рассмотрим
кусок поверхности 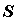 , заданной уравнением , заданной уравнением 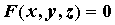 . Пусть
выполняется условие . Пусть
выполняется условие 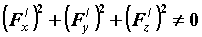 , что означает,
что в каждой точке поверхности существует
нормаль с направляющим вектором , что означает,
что в каждой точке поверхности существует
нормаль с направляющим вектором 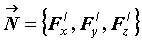 . Выберем одну из
сторон поверхности следующим образом: построим
на поверхности достаточно малый замкнутый
контур, на котором задано направление обхода.
Построим вектор нормали в точке поверхности,
лежащей внутри контура. Если из конца вектора
нормали обход контура кажется происходящим
против часовой стрелки, то будем называть
сторону поверхности, обращенную к вектору
нормали положительной стороной. Таким образом,
будем рассматривать ориентированную
двухстороннюю поверхность, а односторонние
поверхности лист Мебиуса, бутылку Клейна оставим
в покое. Потоком векторного поля . Выберем одну из
сторон поверхности следующим образом: построим
на поверхности достаточно малый замкнутый
контур, на котором задано направление обхода.
Построим вектор нормали в точке поверхности,
лежащей внутри контура. Если из конца вектора
нормали обход контура кажется происходящим
против часовой стрелки, то будем называть
сторону поверхности, обращенную к вектору
нормали положительной стороной. Таким образом,
будем рассматривать ориентированную
двухстороннюю поверхность, а односторонние
поверхности лист Мебиуса, бутылку Клейна оставим
в покое. Потоком векторного поля 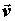 через
ориентированную поверхность называется
поверхностный интеграл по площади поверхности
(1-го рода) через
ориентированную поверхность называется
поверхностный интеграл по площади поверхности
(1-го рода) 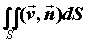 , где - , где - 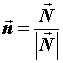 единичный
вектор нормали, направленный в положительную
сторону. Выбор положительной стороны обычно
диктуется физическими условиями задачи. единичный
вектор нормали, направленный в положительную
сторону. Выбор положительной стороны обычно
диктуется физическими условиями задачи.
ПРИМЕР 1. Ориентированные
поверхности.
Непосредственное вычисление потока.
Поскольку поток векторного поля определен с
помощью поверхностного интеграла, вычисление
потока сводится к вычислению такого интеграла от
функции 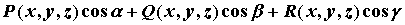 , где , где 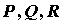 - компоненты векторного поля, - компоненты векторного поля, 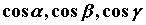 -
направляющие косинусы вектора нормали. -
направляющие косинусы вектора нормали.
ПРИМЕР 2. Вычисление потока
векторного поля.

|

