Векторное поле ~ Векторные
линии (линии тока)
Векторное поле. Если каждой точке 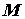 пространства
ставится в соответствие вектор пространства
ставится в соответствие вектор 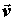 , то говорят, что
задано векторное поле (поле скоростей частиц
движущейся жидкости, силовое поле, поле
электрической напряженности). В декартовой
системе координат векторное поле можно записать
в виде: , то говорят, что
задано векторное поле (поле скоростей частиц
движущейся жидкости, силовое поле, поле
электрической напряженности). В декартовой
системе координат векторное поле можно записать
в виде: 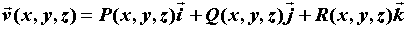 . Скалярные функции . Скалярные функции 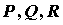 однозначно
определяют векторное поле. Векторное поле может
быть плоским, если однозначно
определяют векторное поле. Векторное поле может
быть плоским, если 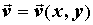 , сферическим, когда , сферическим, когда 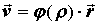 , , 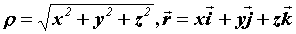 , цилиндрическим,
когда , цилиндрическим,
когда 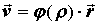 , , 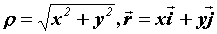 . .
ПРИМЕР 1. Исследование
плоского векторного поля.
Векторные линии (линии тока). Для
наглядного представления векторных полей
используют векторные линии (линии тока). Это
кривые, в каждой точке которых вектор 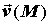 является
касательным вектором. Через каждую точку является
касательным вектором. Через каждую точку 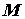 проходит
одна линия тока. За исключением точек, где поле не
определено или проходит
одна линия тока. За исключением точек, где поле не
определено или 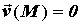 , линии тока никогда не
пересекаются. В декартовых координатах
дифференциальные уравнения линий тока имеют вид: , линии тока никогда не
пересекаются. В декартовых координатах
дифференциальные уравнения линий тока имеют вид:
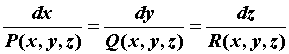
ПРИМЕР 2. Вычисление и
построение векторных линий.

|

