Скалярное поле ~ Поверхности
и линии уровня ~ Производная по
направлению и градиент скалярного поля
Скалярное поле. Если каждой точке 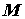 пространства
ставится в соответствие скалярная величина пространства
ставится в соответствие скалярная величина 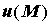 , то
возникает скалярное поле (например, поле
температуры, поле электрического потенциала).
Если введены декартовы координаты, то обозначают
также , то
возникает скалярное поле (например, поле
температуры, поле электрического потенциала).
Если введены декартовы координаты, то обозначают
также
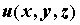 или или
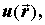
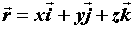 .
Поле может быть плоским, если .
Поле может быть плоским, если 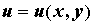 , центральным
(сферическим), если , центральным
(сферическим), если 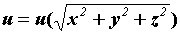 , цилиндрическим,
если , цилиндрическим,
если 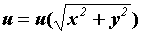 . .
Поверхности и линии уровня. Свойства
скалярных полей можно наглядно изучать с помощью
поверхностей уровня. Это поверхности в
пространстве, на которых 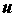 принимает
постоянное значение. Их уравнение: принимает
постоянное значение. Их уравнение: 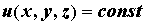 . В
плоском скалярном поле линиями уровня называют
кривые, на которых поле принимает постоянное
значение: . В
плоском скалярном поле линиями уровня называют
кривые, на которых поле принимает постоянное
значение: 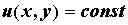 . В отдельных случаях линии уровня
могут вырождаться в точки, а поверхности уровня в
точки и кривые. . В отдельных случаях линии уровня
могут вырождаться в точки, а поверхности уровня в
точки и кривые.
ПРИМЕР 1. Исследование
скалярного поля с помощью линий уровня.

Производная по направлению и градиент
скалярного поля. Пусть 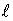 - единичный вектор
с координатами - единичный вектор
с координатами 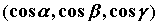 , , 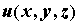 - скалярное поле. Производная по
направлению характеризует изменение поля в
данном направлении и вычисляется по формуле - скалярное поле. Производная по
направлению характеризует изменение поля в
данном направлении и вычисляется по формуле 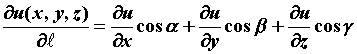 .
Производная по направлению представляет собой
скалярное произведение вектора .
Производная по направлению представляет собой
скалярное произведение вектора 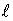 и вектора с
координатами и вектора с
координатами 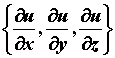 , который называется градиентом
функции , который называется градиентом
функции 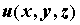 и обозначается и обозначается 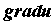 . Поскольку . Поскольку  , где , где
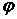 - угол
между - угол
между 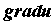 и и 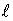 , то вектор , то вектор 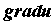 указывает
направление скорейшего возрастания поля указывает
направление скорейшего возрастания поля 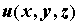 , а его
модуль равен производной по этому направлению.
Так как компоненты градиента являются частными
производными, нетрудно получить следующие
свойства градиента: , а его
модуль равен производной по этому направлению.
Так как компоненты градиента являются частными
производными, нетрудно получить следующие
свойства градиента:
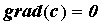
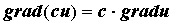
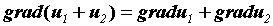
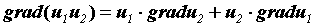
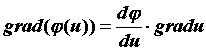
ПРИМЕР 2. Вычисление
производной по направлению скалярного поля.
ПРИМЕР 3. Вычисление
градиента скалярного поля.

|

