Площадь гладкой поверхности
~ Поверхностный интеграл 1-го рода ~ Свойства и вычисление поверхностного
интеграла по площади поверхности
Площадь гладкой поверхности.
Рассмотрим кусок поверхности 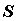 , заданной
уравнением , заданной
уравнением 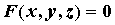 . Пусть выполняется условие . Пусть выполняется условие 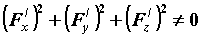 , что
означает, что в каждой точке поверхности
существует нормаль с направляющим вектором , что
означает, что в каждой точке поверхности
существует нормаль с направляющим вектором 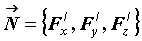 .
Разобьем поверхность .
Разобьем поверхность 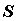 сеткой гладких
кривых на элементарные области сеткой гладких
кривых на элементарные области 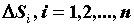 ( разбиение ( разбиение 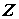 ). Пусть ). Пусть
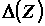 -
наибольший из диаметров элементарных областей.
Если независимо от разбиения -
наибольший из диаметров элементарных областей.
Если независимо от разбиения 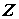 существует существует 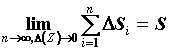 , то он и
называется площадью данной поверхности. Пусть , то он и
называется площадью данной поверхности. Пусть
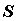 однозначно проектируется на плоскость
однозначно проектируется на плоскость 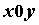 и и 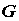 - эта
проекция. Элементу площади - эта
проекция. Элементу площади 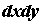 области области 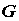 на
плоскости на
плоскости 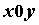 соответствует элемент площади
поверхности соответствует элемент площади
поверхности 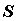 , равный , равный 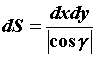 , где , где 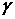 - угол между
нормалью к поверхности - угол между
нормалью к поверхности 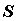 и осью и осью 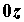 . Поэтому
вычисление площади поверхности сводится к
вычислению двойного интеграла . Поэтому
вычисление площади поверхности сводится к
вычислению двойного интеграла 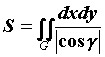 по проекции
поверхности на плоскость. Если поверхность
задана уравнением по проекции
поверхности на плоскость. Если поверхность
задана уравнением 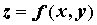 , то , то 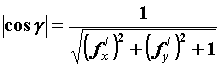 и площадь
поверхности вычисляется по формуле и площадь
поверхности вычисляется по формуле 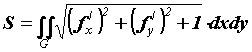 , здесь , здесь 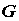 -
проекция поверхности -
проекция поверхности 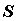 на плоскость на плоскость 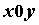 . Если
поверхность однозначно проектируется на другие
координатные плоскости, то соответственно
изменится формула вычисления площади
поверхности. . Если
поверхность однозначно проектируется на другие
координатные плоскости, то соответственно
изменится формула вычисления площади
поверхности.
ПРИМЕР 1. Вычисление площади
поверхности.

Поверхностный интеграл 1-го рода. Пусть
некоторая функция 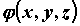 определена и ограничена на гладкой
поверхности определена и ограничена на гладкой
поверхности 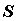 . Выберем разбиение . Выберем разбиение 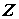 поверхности поверхности 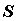 и точки и точки 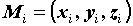 на
каждой элементарной области на
каждой элементарной области 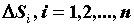 и составим
интегральную сумму и составим
интегральную сумму 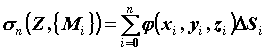 . Если независимо от выбора
разбиения . Если независимо от выбора
разбиения 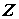 и точек и точек 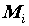 существует существует 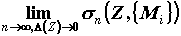 , то он
называется поверхностным интегралом по площади
поверхности , то он
называется поверхностным интегралом по площади
поверхности 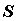 (1-го рода) от функции (1-го рода) от функции 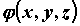 и обозначается и обозначается
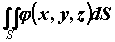 . .
Свойства и вычисление поверхностного
интеграла по площади поверхности. Если
поверхность задана уравнением 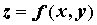 и однозначно
проектируется на плоскость и однозначно
проектируется на плоскость 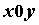 , то поверхностный
интеграл 1-го рода вычисляется по формуле , то поверхностный
интеграл 1-го рода вычисляется по формуле 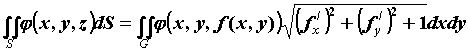 .
Нетрудно получить аналогичные формулы, если
поверхность однозначно проектируется на другие
координатные плоскости. Поскольку вычисление
поверхностного интеграла сводится к двойному
интегралу, то, естественно, все свойства
поверхностного интеграла 1-го рода такие же, как и
у двойного. .
Нетрудно получить аналогичные формулы, если
поверхность однозначно проектируется на другие
координатные плоскости. Поскольку вычисление
поверхностного интеграла сводится к двойному
интегралу, то, естественно, все свойства
поверхностного интеграла 1-го рода такие же, как и
у двойного.
ПРИМЕР 2. Вычисление
поверхностного интеграла по площади
поверхности.

|

