Замена переменных в двойном
интеграле ~ Замена переменных в тройном
интеграле ~ Двойной интеграл в полярных
координатах
Замена переменных в двойном интеграле.
Пусть функции 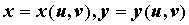 взаимно однозначно отображают
открытое множество, содержащее область взаимно однозначно отображают
открытое множество, содержащее область 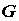 плоскости плоскости
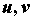 на
открытое множество, содержащее область на
открытое множество, содержащее область 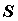 , и пусть , и пусть 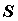 является
образом является
образом 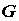 . Если . Если 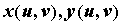 и их частные производные
непрерывны, а определитель и их частные производные
непрерывны, а определитель 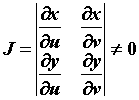 , то , то 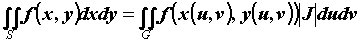 . Выражение . Выражение 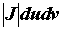 называется элементом площади в криволинейных
координатах, функциональный определитель
называется элементом площади в криволинейных
координатах, функциональный определитель 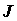 -
якобианом. -
якобианом.
ПРИМЕР 1. Вычисление
якобиана для полярных и обобщенных полярных
координат.

Вычисление площади.
Замена переменных в тройном интеграле.
Пусть посредством функций 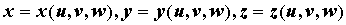 производится
взаимно однозначное отображение открытого
множества, содержащего область производится
взаимно однозначное отображение открытого
множества, содержащего область 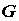 пространства пространства 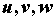 на
открытое множество, содержащее область на
открытое множество, содержащее область 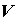 пространства пространства
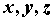 и и 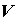 есть
образ есть
образ 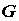 .
Если эти три функции непрерывны вместе со своими
первыми частными производными в области .
Если эти три функции непрерывны вместе со своими
первыми частными производными в области 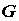 и якобиан и якобиан
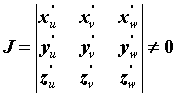 , то , то 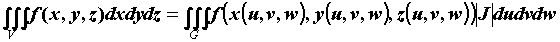 .
Выражение .
Выражение 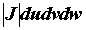 называется элементом объема в
криволинейных координатах . называется элементом объема в
криволинейных координатах .
ПРИМЕР 2. Вычисление
якобиана для цилиндрических и сферических
координат.

Вычисление объема.
Двойной интеграл в полярных координатах.
Введем на плоскости полярные координаты. Пусть 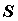 - область,
полученная взаимно однозначным отображением
области - область,
полученная взаимно однозначным отображением
области 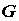 плоскости плоскости 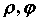 , определяемым
функциями , определяемым
функциями 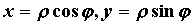 . Тогда . Тогда 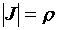 , а двойной интеграл в полярных
координатах вычисляется по формуле: , а двойной интеграл в полярных
координатах вычисляется по формуле: 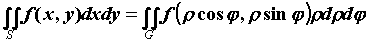 .Элемент площади в
полярных координатах есть .Элемент площади в
полярных координатах есть 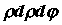 . .
ПРИМЕР 3. Вычисление
двойного интеграла в полярных координатах.

|

